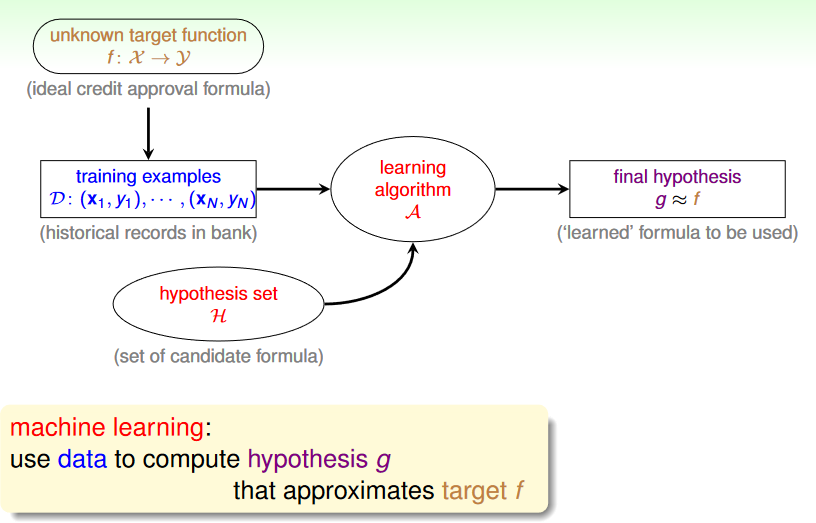
Recap

目標：判斷該不該給一個用戶核發信用卡

source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/01u_handout.pdf p.21

Perceptron Hypothesis Set

對每一筆 $\bf x$ 我們都計算一筆權重分數，然後根據有沒有大於 threshold 來通過或拒絕，換成數學式如下:

$h({\bf x}) = \text{sign}\left(\left(\sum^d_{i=1}{\color{red} w_i}x_i\right) - \text{\color{red} threshold}\right), h \in \mathcal{H}$

如此一來，輸出 $Y$ 就變成只有 1 (good) 和 -1 (bad)

用矩陣表達

我們可以將上面的式子化成矩陣來表示，透過將 threshold 視為權重的一部份($w_0$)，並將 $x_0$ 設為 1，就能得到下列的數學式:

source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/02u_handout.pdf p.4

Notation Conventions

• traning examples $\mathcal{D}$ size: $n = 1, 2, \cdots, N$
• features size: $i = 0, 1, \cdots, d$
• ${\bf x} = (x_0, x_1, \cdots, x_d)$: an input vector
• ${\bf x}_n = (x_{n,1}, x_{n,2}, \cdots, x_{n,d})$: the $n$-th vector in $\mathcal{D}$
• $\bf w$ 和 ${\bf w}_t$ 同理

從空間視角來看

如果我們放在空間中來看:

• featrues $\bf x$: points in $\mathbb{R}^d$
• labels $y$: +1 或 -1 (用顏色表示)
• perceptron $h$: $\mathbb{R}^d$ 中的超平面 (可以將空間一分為二的邊界) 我們的目的就是找到一個 $h$ 可以很剛好地把 $y = h({\bf x})$ 不同的 $\bf x$ 們分開

$y$ 只有兩種，所以 perceptrons 其實就是 linear binary classifiers

Perceptron Learning Algorithm (PLA)

如何在 $\mathcal{H}$ (所有可能的 perceptrons) 裡面找到一個 $g$，讓這個 $g$ 和 $f$ (理想中的完美函數) 盡可能地接近？

註: 由於 perceptron $g_t$ 內的需要設定的數值只有 ${\bf w}_t$，因此接下來直接用 ${\bf w}_t$ 來表示 $g_t$

PLA 流程

從 ${\bf w}_0$ (零向量) 開始，$t = 0, 1, \cdots$

第一步: 找 mistake
使用 ${\bf w}_t$ 進行分類，找到一個 mistake $({\bf x}_t, y_t)$，也就是

$\text{sign}\left({\bf w}^T_t{\bf x}_t\right) \ne y_t$

第二步: 更新 $\bf w$
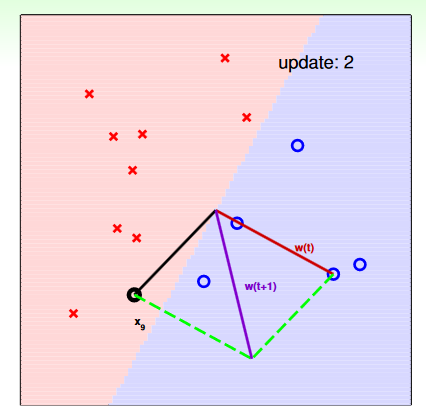
如下圖，如果 $y_t = +1$，但 sign 的結果是 -1，即 ${\bf w}^T_t{\bf x}_t \lt 0$，也就是說 $\bf w$ 和 $\bf x$ 的夾角大於 90 度，分類錯了，因此我們必須將 $\bf w$ 旋轉讓夾角小於 90。更新的方法就是直接做向量的合成:

${\bf w}_{t+1} \leftarrow {\bf w}_t + y_t{\bf x}_t$

${\bf w}$ 實際上表示的是 $g$ (分類線) 的法向量，因此如果 $\bf x$ 和 $\bf w$ 的夾角小於 90 度，也就是 ${\bf w}^T_t{\bf x}_t \gt 0$，則分類為 +1，反之亦然。

source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/02u_handout.pdf p.13

就這樣直到找不到 mistake 為止

sign = 0 怎麼辦

當 sign = 0 的時候，實際上有許多種處理方法，每個人都有自己的慣例:

• 將 sign(0) 視為 -1
• 將 sign(0) 視為 +1
• 直接更新

實際上除了 ${\bf w}_0$ 會出現這種情況外，其餘要發生 sign = 0 的機會不高

Cyclic PLA

上面的流程還有問題沒有解決: 怎麼找 mistake? 如果有很多個 mistake 怎麼辦? 實務上，常用的方法是遍歷每個點，從 ${\bf x}_1$ 到 ${\bf x}_n$，遇到 mistake 就更新，直到遍歷了每個點都沒有找到 mistake 為止，這種方法稱為 cyclic PLA。

Linear Separability

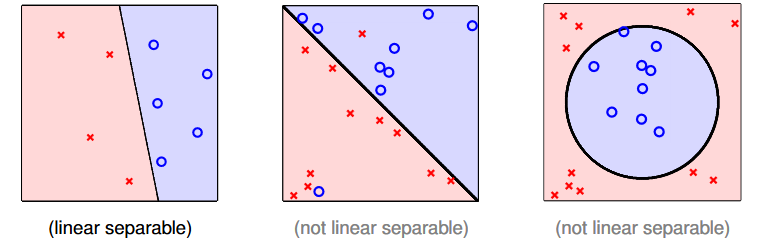
PLA 基本上只適用於可以線性二分的 $\mathcal{D}$，如下圖所示:

source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/02u_handout.pdf p.15

證明 PLA 會停止

假設 $\mathcal{D}$ linear separable，也就是說一定有一個 ${\bf w}_f$ 使得 $y_n = \text{sign}\left({\bf w}^T_f{\bf x}_n\right)$ 因為可以完美分類，代表每一個 ${\bf x}_n$ 和 ${\bf w}_f$ 的夾角都大於 0:

$y_t{\bf w}^T_f{\bf x}_t \ge \min_n y_n{\bf w}^T_f{\bf x}_n \gt 0$

然後，我們可以從更新的式子中推出，每一次更新，${\bf w}_t$ 都會更靠近 ${\bf w}_f$ (夾角越小):

w 的(長度)成長速率

${\bf w}_t$ changed only when $\text{sign}\left({\bf w}^T_t{\bf x}_t\right) \ne y_t \iff y_t{\bf w}^T_t{\bf x}_t \le 0$ 因此我們可以推出，$\bf w$ 的成長幅度不會超過用來更新的 $\bf x$ 的長度，也不會超過最長的 $\bf x$ 的長度:

PLA Bound

從上面兩個推導可以知道

• 內積的成長速率快: ${\bf w}^T_f{\bf w}_{t+1} \ge {\bf w}^T_f{\bf w}_t + \color{blue}\min_n y_n{\bf w}^T_f{\bf x}_n$
  藍色替換成 ${\color{blue}\rho}\cdot\lVert{\bf w}_f\rVert$
• 長度的成長速率慢: $\lVert{\bf w}_{t+1}\rVert^2 \le \lVert{\bf w}_t\rVert^2 + \color{red}\max_n\lVert {\bf x}_n\rVert^2$
  紅色替換成 $\color{red}R^2$

在 $T$ 次更新後

• ${\color{blue}{\bf w}^T_f{\bf w}_T \ge}\ {\bf w}^T_0{\bf w}_0 + T\cdot\rho\cdot\lVert{\bf w}_f\rVert = \color{blue}T\cdot\rho\cdot\lVert{\bf w}_f\rVert$
• ${\color{red}\lVert{\bf w}_T\rVert^2 \le}\ \lVert{\bf w}_0\rVert^2 + T\cdot R^2 = \color{red}T\cdot R^2$

接著就可以發現 ${\bf w}_f$ 和 ${\bf w}_T$ 的 cos 夾角會有 lower bound，而且更新次數 $T$ 有 upper bound

${{\color{blue}{\bf w}^T_f} \over \lVert{\bf w}_f\rVert}{{\color{blue}{\bf w}_T} \over {\color{red}\lVert{\bf w}_T\rVert}} \ge {{\color{blue}T\cdot\rho}\cdot\lVert{\bf w}_f\rVert \over \lVert{\bf w}_f\rVert\cdot{\color{red}\sqrt{T}\cdot R}} \implies T \le \left({R \over \rho}\right)^2$

Overview

優點: 簡單、快速、適用於任何維度 缺點:

• $\mathcal{D}$ 需要 linear separable (而且我們通常不會知道)
• 因為 $\rho$ depends on ${\bf w}_f$，不能確定什麼時候會停 (雖然如果會停的話通常很快就會停)

PLA with noisy data

如果我們的 $\mathcal{D}$ 是有雜訊的 (不是 linear separable)，我們或許可以讓 PLA 多一點容忍度，只要「大多數」的 $\bf x$ 都有符合 $f({\bf x}_n) = y_n$ 就好，因此我們的目標就是找到 mistake 最少的那個 $g$ 就好:

${\bf w}_g \leftarrow \arg\min_w \sum^N_{n=1}\left[\left[y_n \ne \text{sign}({\bf w}^T{\bf x}_n)\right]\right]$

然而，這是一個 NP-hard 問題