Learning is Impossible?

假設我們現在要對 $\mathcal{X} = \{0,1\}^3$ 做 binary classification，然後 $\mathcal{H}$ 是所有可能的函數。而我們可以找到了一個 $g \in \mathcal{H}$，在 $\mathcal{D}$ 的範圍內符合 $g \approx f$，在 $\mathcal{D}$ 的範圍外的輸出是 "O X O"，那我們要如何知道(在 $\mathcal{D}$ 的範圍外)是否符合 $g \approx f$ 呢？ 因為 $f$ (理想的函數)是未知的，而且有很多可能: 如果理想的函數是 $f_3$，那 $g \approx f$ 就成立；但如果是 $f_5$，則 $g$ 就變成了反指標。 因此，我們很難透過在 $\mathcal{D}$ 內學習，來推斷 $\mathcal{D}$ 外面的東西。

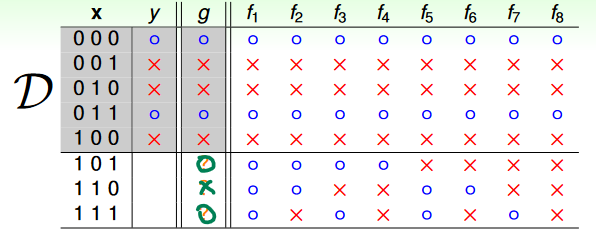source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/04u_handout.pdf p.7

No Free Launch Theorem

Without any assumptions on the learning problem on hand, all learning algorithms perform the same

也就是說，對於任何 learning problem，(在沒有任何限制的情形下)我們都沒有辦法找到一個 best (or worst) algorithm

如何推斷未知

Hoeffding's Inequality

假設有一桶球，裡面包含了藍球和紅色球，我們要如何在不計算全部球的情況下，知道紅色球的占比(拿出紅色球的機率) $\mu$？

在學統計的時候，我們知道可以取一些 sample 出來，計算 sample 內紅色球的占比 $\nu$，那我們可以從已知的 $\nu$ 去推斷未知的 $\mu$ 嗎？

Hoeffding's Inequality 告訴我們，當 sample size $N$ 夠大的時候，$\nu$ 確實有可能接近 $\mu$ ($\epsilon$ 為自訂的誤差):

$\mathbb{P}[|\nu-\mu|\gt\epsilon] \le 2 \exp\left(-2\epsilon^2N\right)$

也就是說 $\nu = \mu$ 這個 statement 是 PAC: probably (有可能剛好 sample 的分布和實際分布差超多，但機會不大) approximately ($\nu$ 和 $\mu$ 之間會有誤差但小於 $\epsilon$) correct

Connect to Learning Problem

在球的例子中:

• 從桶子內取出 size-$N$ 的 sample
• 判斷 sample 內每個球分別是紅色還是藍色
• 計算 sample 內紅色球的占比 $\nu$
• 推斷從桶子內隨機拿一顆球，是紅色球的機率 $\mu$

換成 learning problem: (假設已經得到一個 $h$)

• 從 $\mathcal{X}$ 內取一個 size-$N$ 的 $\mathcal{D}$

• 判斷 $\mathcal{D}$ 內的每個 $\bf x$ 分別是 $\color{red} h({\bf x}) \ne y_n$ 還是 $\color{blue} h({\bf x}) = y_n$

• 計算 $\mathcal{D}$ 內 $\color{red} h({\bf x}) \ne y_n$ 的占比 (in-sample error)

  $E_{\text{in}}(h) = {1 \over N}\sum_{n=1}^N[[h({\bf x}_n) \ne y_n]]$

• 推斷從 $\mathcal{X}$ 內隨機拿一個 $\bf x$，而 $\color{red} h({\bf x}) \ne f({\bf x})$ 的機率 (out-of-sample error)

  $E_{\text{out}}(h) = \mathbb{E}_{x \sim P}[[h({\bf x}) \ne f({\bf x})]]$

  這裡的 $P$ 是 $X$ (所有可能 input)的機率分布

註: 這裡的 $[[]]$ 是 Iverson bracket，如果滿足括號內條件則為 1，反之為 0

也就是說，即便在不知道 $E_{\text{out}}(h)$ 的情況下 ($f$ 和 $P$ 都未知)，我們也能說 $E_{\text{in}}(h) = E_{\text{out}}(h)$，因為這個 statement 是 PAC，而且 $\mathcal{D}$ 越大 statement 成立的可能性越高。

應用到真實的 Learning Problem

上面的推論都是基於一個 $h$ 的情形，但在真正的機器學習時，$\mathcal{H}$ 內不會只有一個 $h$，當 $h$ 變多會產生什麼影響呢？

For Multiple h

先考慮一個問題，假設一般硬幣 $f$ 的丟到正面的機率是 $1 \over 2$，現在有 150 個人，每個人都重複丟硬幣 5 次，而其中有一個人連續 5 次都丟到正面，則我們是否可以推斷他的硬幣 $h$ 丟到正面的機率比一般硬幣大很多？

答案是否定的，透過簡單的數學我們可以知道，都是一般硬幣的情況下，在 150 人中有其中一人連續 5 次丟到正面的機率仍是 $1 - ({31 \over 32})^150 > 99\%$，也就是說，硬幣 $h$ 有極大可能還是個一般硬幣 $f$。

推廣回機器學習，即便每個 $h$ 都是正常的 ($h \approx f$)，一旦 $\mathcal{H}$ 變大 (取出的 $h$ 變多)，則出現一個 $h$ 讓 $E_{\text{in}}(h)$ 和 $E_{\text{out}}(h)$ 相差甚遠也是很有可能的，也就是說我們不能用該 $E_{\text{in}}(h)$ 去推論 $E_{\text{out}}(h)$。更何況 $\mathcal{H}$ 通常是 infinite 的。

什麼樣的情況才能讓我們不管拿到什麼 $h$ 都可以符合 $E_{\text{in}}(h) = E_{\text{out}}(h)$ 的推論呢？

Chance to get lucky data

先介紹一下 bad data，bad data 指的是利用這筆 $\mathcal{D}$ 所算出來的 $E_{\text{in}}(h)$ 很小，但實際上的 $E_{\text{out}}(h)$ 很大，也就是說我們不能用這個 $E_{\text{in}}(h)$ 來推論 $E_{\text{out}}(h)$。

由於 Hoeffding 保證的實際上是，從 $\mathcal{X}$ 中取了很多樣本 $\mathcal{D}$ 時， bad data 的占比很低 (所以 $E_{\text{in}} = E_{\text{out}}$ 是 PAC)，也就是表格中的每一個 row。

當今天有很多 $h$ 的時候，我們希望的是找到一個 lucky data ($\mathcal{D}_{1126}$): 對於每一個 $h$ 而言都不是 bad data ($E_{\text{in}}(h) = E_{\text{out}}(h)$ 是 PAC)，如此一來不管我們取出什麼 $h$ 都可以用 $E_{\text{in}}(h)$ 來推論 $E_{\text{out}}(h)$。

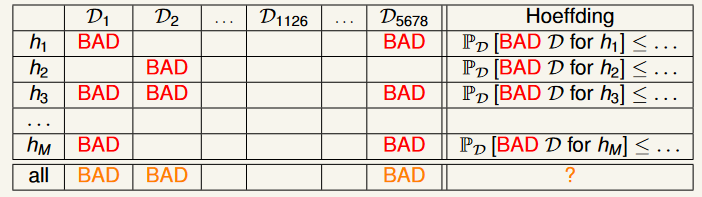source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/04u_handout.pdf p.26

因此我們要做的就是去計算從 $\mathcal{X}$ 內得到 lucky data 的機會是多少，或是換句話說，沒有得到 lucky data = 得到 bad data 的機會有多大:

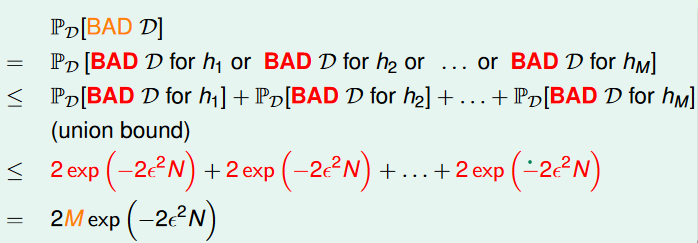source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/04u_handout.pdf p.27

上面的式子稱為 finite-bin version of Hoeffding

因此，對於任何 $M$ ($\mathcal{H}$ 的大小)、$N$ ($\mathcal{D}$ 的大小)、$\epsilon$ (自訂誤差門檻) 而言，即便不知道 $E_{\text{out}}(h_m)$，我們也能夠說每個 $h_m$ 都符合 $E_{\text{in}}(h) = E_{\text{out}}(h)$ 是 PAC 的推論。

Statistical Learning Flow

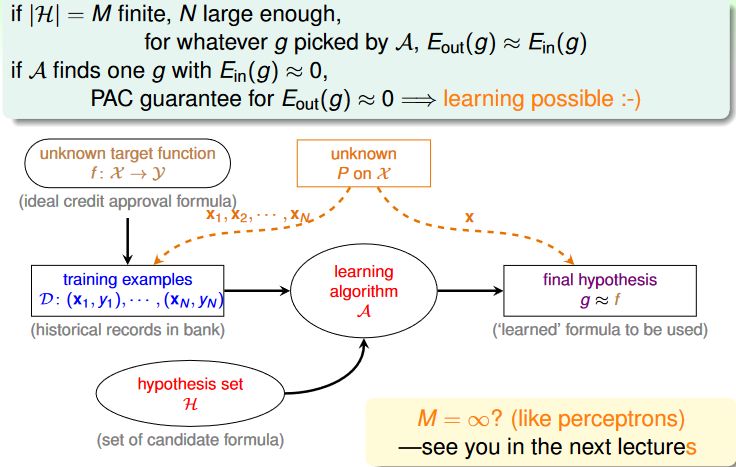source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/04u_handout.pdf p.28

到目前為止，我們可以將機器學習的流程更改成上面的樣子，然而注意這是在 $\mathcal{H}$ 的大小是有限大的情形下。