Recap
由於 lecture 6 被跳過了,所以這裡先講講 lecture 6 的結論。
-
當 mH(N) 有 break point k 時 (N≥2,k≥3),我們會得到 upper bound:
mH(N)≤B(N,k)=∑i=0k−1(iN)≤Nk−1
也就是說我們有夠小的 H
-
透過一串騷操作,我們可以將原本「得到 bad data 的機會」的 upper bound 換成 (which is called VC bound):
≤≤≤PD[∣Ein(g)−Eout(g)∣>ϵ]PD[∃ h∈H s.t. ∣Ein(h)−Eout(h)∣>ϵ]4mH(2N)exp(−81ϵ2N)4(2N)k+1exp(−81ϵ2N)
綜合以上兩點,當 ==mH(N) 有 break point k 且 N 足夠大的時候,我們就能說 Eout≈Ein is possible。==
然後當 A 可以從 H 裡挑出一個好的 g (有小的 Ein),我們就能說 Eout 應該也是小的,因此 g 可能相當接近理想中的 f。
VC Dimension
VC Dimension dvc(H) 的定義為:
largest N for which mH(N)=2N (也就是 maximum non-break point,H 可以 shatter 的最大 input 數)
VC Dimension and Learning
從定義我們可以得到: if N≥2,dvc≥2, mH(N)≤2dvc
因此當我們能找到 finite 的 dvc 時,就代表任何 g 都會符合 Ein(g)≈Eout(g)
此時我們需要考慮的就只剩下 H 了:
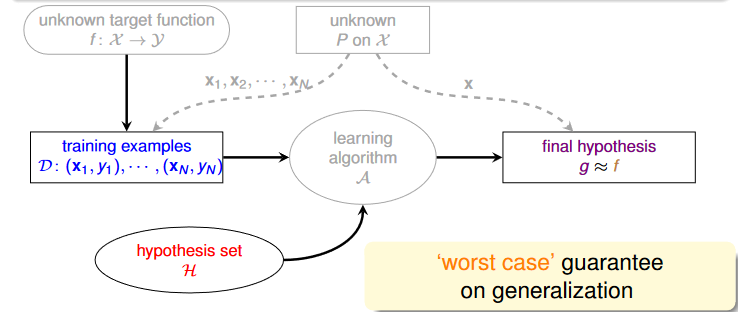 source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.6
source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.6
VC Dimension of Perceptrons
到目前為止,我們已經證明了 2D PLA 是可行的:
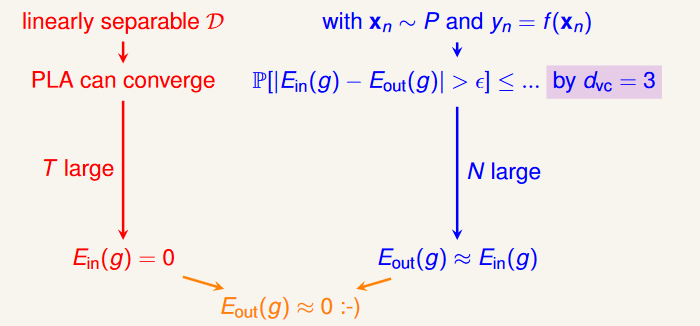 source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.8
source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.8
接下來,我們要來找出當 x 的有超過兩個 features 時,dvc 應該長怎樣。
根據經驗,我們可以假設 d-D perceptrons 的 dvc=d+1,我們分成兩部分來證明這個式子。
證明 dvc≥d+1
也就是說,我們可以 shatter 某些 d+1 inputs 組合。
我們先假設一個特殊的有 d+1 個點的 input X:
X=−x1T−−x2T−−x3T−⋮−xd+1T−=111⋮ 1010⋮ 0001⋯⋯⋯⋱000001
如果很難想像的話,在 2D (d=2) 的時候,這個 X 在空間中會長這樣:
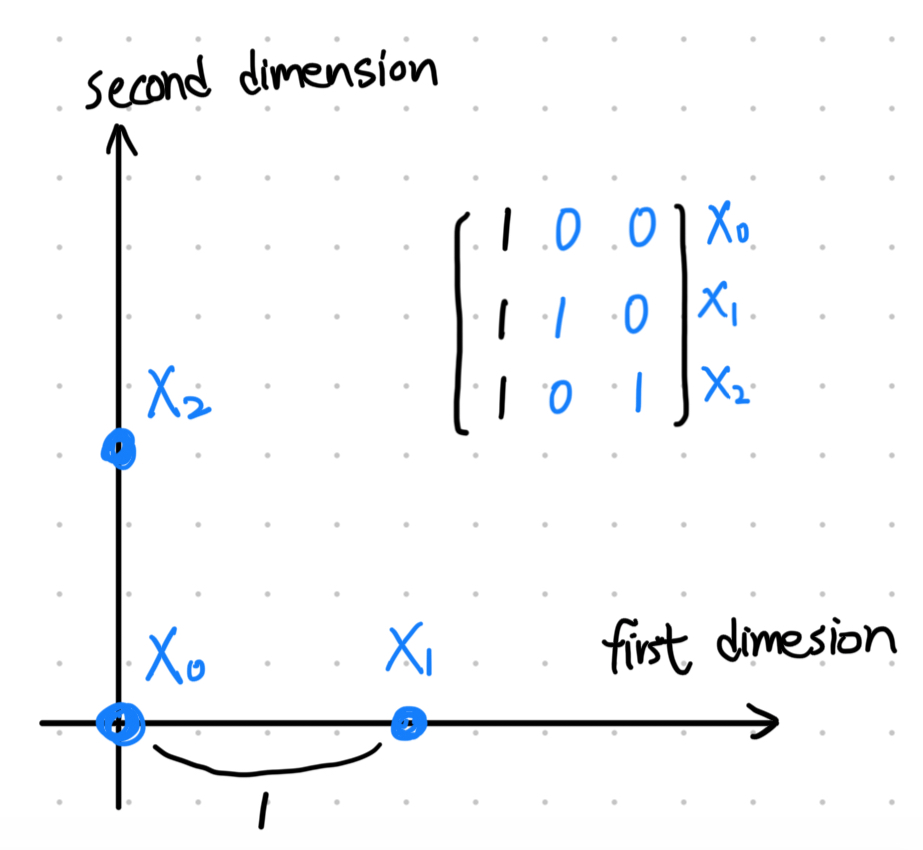 source: my ipad :)
source: my ipad :)
由於這個 X 是可逆的,所以不管 y 長怎樣,我們都能夠讓 w=X−1y,這樣一來 sign(Xw)=y,也就是說這個 X 是可以被 shatter 的,因此 dvc≥d+1。
證明 dvc≤d+1
考慮有 d+2 個點的 general X:
X=−x1T−−x2T−−x3T−⋮−xd+1T−−xd+2T−
由於 rows (d+2) 比 columns (d+1) 還多,所以我們要考慮 linear dependence 的問題:
xd+2=a1x1+a2x2+⋯+ad+1xd+1
其中 ai 代表該 xi 的 sign。
現在假設只有 a1 是 +1,其他 a2 到 ad+2 都是 −1 的情況,我們會發現如果有個 w 可以準確分類 x1 到 xd+1 的話,則該 w 就不可能讓 xd+2 被分類正確:
wTxd+2=a1wTx1+a2wTx2+⋯+ad+1wTxd+1>0
因此,在有 d+2 個點的情況下,不管 X 長怎樣,一定都會有一個 y 找不到對應的 w,因此不能被 shatter,也就是說 dvc≤d+1。
解讀 VC Dimension
Degrees of Freedom
degrees of freedom (DOF) 代表在 hypothesis function h 內的 independent parameters 的數量,通常這會和 h 的 parameters w 的維度相近,但不一定相等。
舉例來說,假設模型有三個參數 β1,β2,β3,但我們加了一個約束條件:
β1+β2+β3=1
因此 β3 必須根據 β1,β2 的選擇來計算,也就是說我們不能「自由」的調整它,因此雖然 w 的維度是 3,但是 DOF 卻是 2。
DOF 越高,代表模型越靈活,越能夠擬合資料,但有可能 over-fitting。
Powerfulness of H
有了 DOF 的概念,(在 binary classification 上) dvc(H) 的意義相當於是一個 H 的effective DOF,於是,我們可以用 dvc(H) 來衡量一個 H (在 binary classification 上) 的能力有多強。
所謂的 effective DOF 是指最後真正對模型產生影響的 independent parameters 的數量,通常會和 DOF 相近,但不一定相等。
當然,在 PLA 的例子裡,w 的維度 = DOF = Effective DOF = dvc = d+1
Trade-off on VC Dimension
Lecture 5 的一開始我們有提到兩個問題:
- 如果確保 Ein 和 Eout 足夠接近?
- 如何讓 Ein 足夠小?
這兩個問題除了和 M (size of H),也和 dvc 有關:
- small dvc:
- Yes: 誤差 ≤4(2N)dvcexp(⋯)
- No: 能力不夠強
- large dvc:
因此選擇合適的 dvc (or H) 相當重要。
Penalty for Model Complexity
回到這個式子:
PD[∣Ein(g)−Eout(g)∣>ϵ]≤4(2N)dvcexp(−81ϵ2N)
我們現在將右項替換成 δ (confidence level),然後做一些轉換可以得到 Ein 和 Eout 的誤差實際上會等於:
ϵ=N8ln(δ4(2N)dvc)
這誤差又叫做 generalization error,而我們又再給他一個更簡單的代號:
N8ln(δ4(2N)dvc)=Ω(N,H,δ)
而這個 Ω 被稱為 penalty for model complexity。
The VC Message
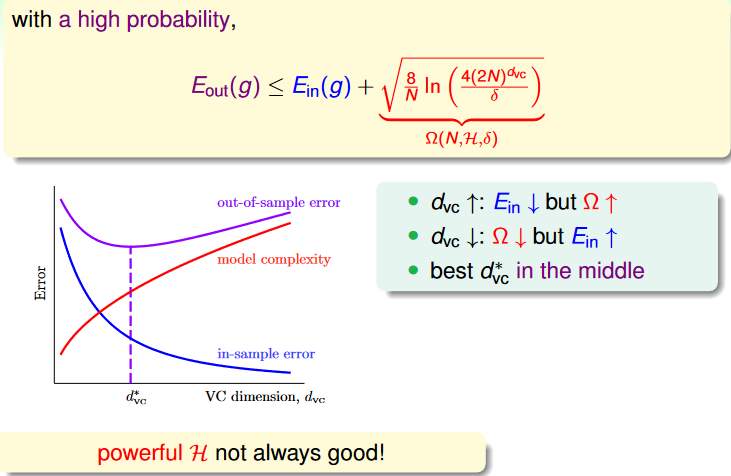 source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.22
source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.22
Sample Complexity
現在假設條件 ϵ=0.1,δ=0.1,dvc=3,則我們需要多少 sample 才能讓
4(2N)dvcexp(−81ϵ2N)≤δ (誤差的 upper bound 在信任水準內)。
理論上而言,我們需要 N=29300 才能讓 upper bound 為 9.99×10−2,也就是需要 N≈10000dvc。
不過,實務上大概只要抓 N≈10dvc 就夠了,為什麼?
 source: https://www.youtube.com/live/3zbhL1Q7nu0 p.24
source: https://www.youtube.com/live/3zbhL1Q7nu0 p.24
 source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.6
source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.6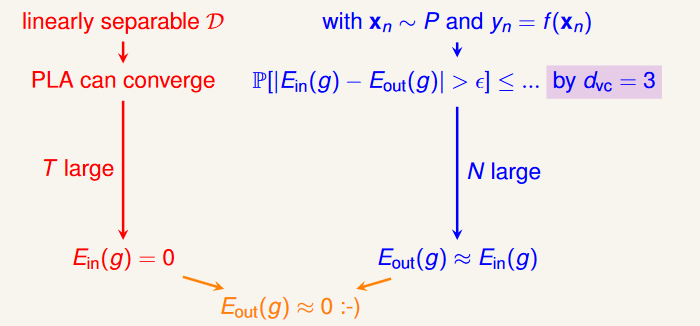 source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.8
source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.8 source: my ipad :)
source: my ipad :) source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.22
source: https://www.csie.ntu.edu.tw/~htlin/course/ml24fall/doc/07u_handout.pdf p.22 source: https://www.youtube.com/live/3zbhL1Q7nu0 p.24
source: https://www.youtube.com/live/3zbhL1Q7nu0 p.24