blog logo
Blog
李宏毅機器學習筆記 (一) - 機器學習概觀

早上好暑假，現在我有李宏毅教授的【機器學習 2021】系列影片，因為非常好影片，內容非常好。
以下是本篇筆記所參考的影片：
【機器學習2021】預測本頻道觀看人數 (上) - 機器學習基本概念簡介 (youtube.com)
【機器學習2021】預測本頻道觀看人數 (下) - 深度學習基本概念簡介 (youtube.com)

機器學習 = 讓機器找到特定的 function

這些 function 可以是:

  • Regression: function 的輸出是一個數值
  • Classification: 給定選項，function 會輸出正確的選項
  • Structured Learning: function 會產生一個有結構的物件 (ex: 圖片、文件)

如何讓機器找 (regression) function?

假設我們想要找一個 function 是 f(今天的觀看次數)=明天的觀看次數f(\text{今天的觀看次數}) = \text{明天的觀看次數}

第一步: 猜 Function with Unknown Parameters

首先，我們可以基於 domain knowledge 去「猜測」function 的形式。 假設我們「猜測」 function 的形式是

y=b+wx1y = b + wx_1

這裡的 x1x_1 是 Feature，是我們已經知道的數據，在這個例子中我們將其定為昨天的觀看次數，bb 和 ww 則分別稱為 Bias 和 Weight。最後我們會將這種帶有未知函數的 function 稱為 Model。

第二步: 從訓練資料定義 Loss

Loss L(b,w)L(b, w) 也是一個 function，它代表的意義是判斷一組未知參數 (bb, ww) 有多好。 Loss 的形式是由我們自己定義的，舉個例子，我們可以先計算 y=b+wx1y = b + wx_1 (我們預設的 function 用這組參數算出來的結果) 和 y^\hat{y} (實際上的結果，又被稱作 Label) 的差距:

e=∣y−y^∣e = |y - \hat{y}|

然後將 Loss 定義成每筆差距的總和:

L(b,w)=1N∑enL(b, w) = {1 \over N}\sum e_n

上面這種方法定義出來的 Loss 被稱為 mean absolute error (MAE)，而如果改成 e=(y−y^)2e = (y - \hat{y})^2 的話，這種 Loss 被稱為 mean square error (MSE)。

第三步: Optimization - 找到一組有最小 Loss 的參數

註：雖然標題是說最小，但實際上是要找最「好」的，這取決於你對 Loss 的定義，有可能在某些定義下 Loss 是越大越好。

在這個階段，我們需要找到一組參數 (w∗,b∗)(w^*,b^*)，他們算出來的 L(w∗,b∗)L(w^*,b^*) 是最小的。

註：以下只介紹了 gradient descent 這個方法，不過要找參數其實還有更多方法。

先假設 Loss 的參數變成只剩下 ww L(w)L(w)

隨機挑一個 w0w_0 當作起點，然後計算微分

dLdw∣w=w0{dL \over dw}|_{w = w_0}

也就是圖中的藍色切線的斜率，因此我們就可以知道哪邊的 Loss 會比較小。 接著我們就往比較小的那邊移動一個距離，計算下一個 w1w_1:

w1=w0−η dLdw∣w=w0w_1 = w_0 - \eta\ {dL \over dw}|_{w = w_0}

這裡的 η\eta 是所謂的 Learning Rate，它是一個 hyperparameters，也就是我們在訓練的過程中需要手動調整的參數。如果 η\eta 太大，就有可能錯過某些點，反之如果太小，訓練的步數就會增加。

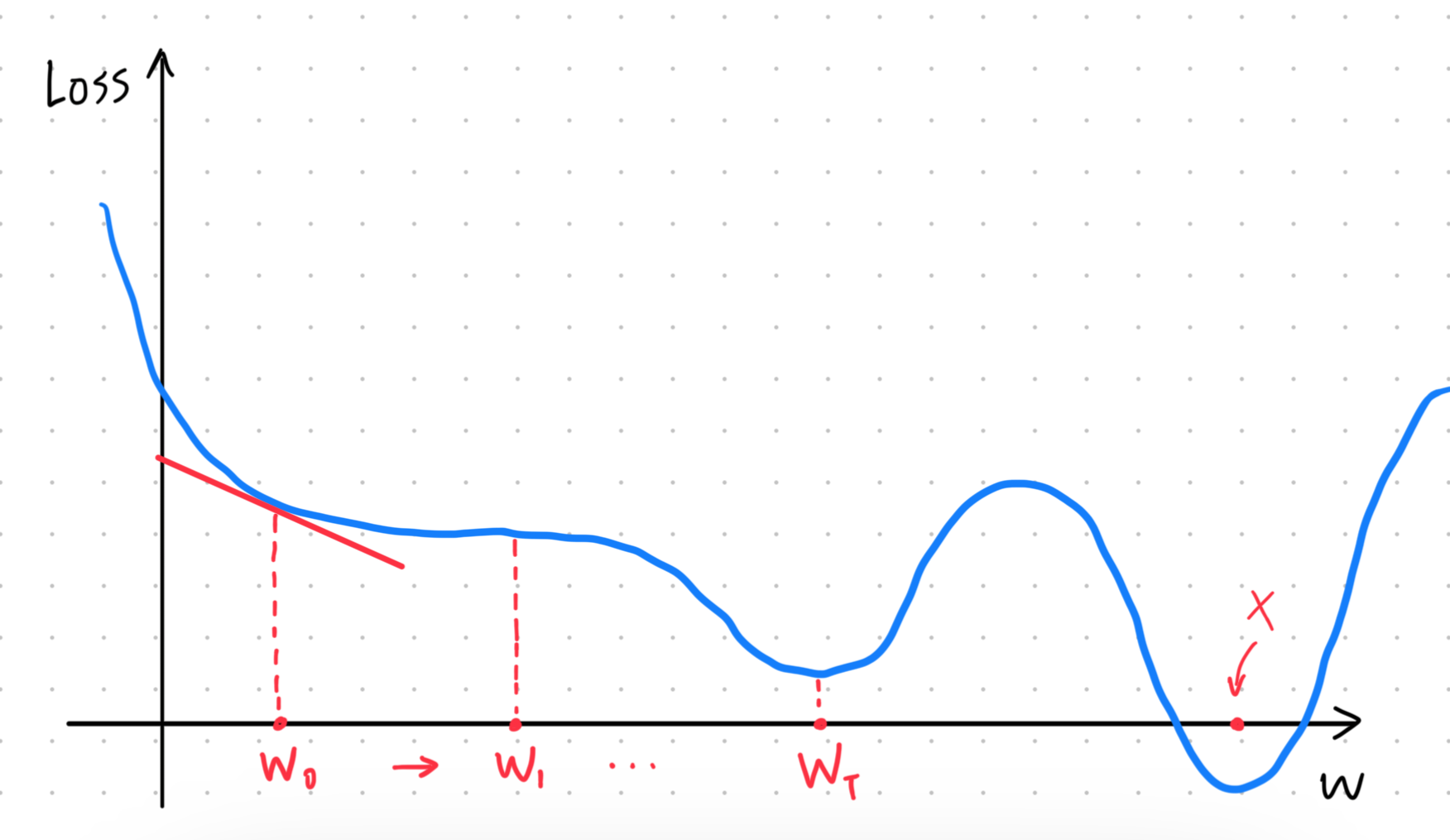
接下來就是不斷的反覆以上步驟，直到在某個地方停下來。理想的情況下，當 dLdw=0{dL \over dw} = 0 的時候 (也就是圖中 wTw_T 對應的點)，無論 η\eta 多大，移動的距離都會是 0，所以就會自然地停止。此時我們將 wTw_T 對應的 Loss 稱為 local minima，因為實際上圖中最小的 Loss，也就是 global minima 是出現在 X 點。

註: local minima 的問題其實是一個假議題，實際上 gradient descent 真正的痛點不在這裡，詳情可以見機器學習筆記 (三)

然而實際上不會每次都剛好移動到那個點，所以大多數的情況是我們會幫移動次數設上一個限制，當移動一定次數後就會停止，否則我們有可能不斷的移動下去都找不到 minima。

回到原本兩個參數的 L(b,w)L(b, w)，運作模式也是一樣的，只不過算微分的時候要變成

w1=w0−η dLdw∣w=w0,b=b0w_1 = w_0 - \eta\ {dL \over dw}|_{w = w_0, b = b_0} b1=b0−η dLdb∣w=w0,b=b0b_1 = b_0 - \eta\ {dL \over db}|_{w = w_0, b = b_0}

用測試資料驗證

在使用了訓練數據 (2019-2022 年每天的觀看次數) 找出了一個 function:

y=b∗+w∗x1y = b^* + w^* x_1

之後，接下來要做的就是用測試資料 (2023 年每天的觀看次數) 來驗證我們的 function 能不能正確預測訓練資料外的情況 (一樣也是透過計算 Loss)。

當然，我們可以不只考慮昨天的觀看次數，如果我們要用前七天的觀看次數對明天的觀看次數，那我們就可以把 function 假設成

y=b+∑j=17wjxjy = b + \sum^7_{j=1}w_jx_j

其中 xjx_j 就是每一天的觀看次數。

上面我們得出來的形式為

y=b+∑jwjxjy = b + \sum_j w_j x_j

的 model，就是所謂的 Linear model。 然而，因為 Linear model 無論如何都是一條直線，因此可能沒有辦法模擬出真實的情況，這種來自於 model 本身的限制被稱為 Model Bias。

讓機器找 function (但 model 更複雜)

為了減低 model bias，我們需要讓 model 更複雜，那該怎麼做呢？

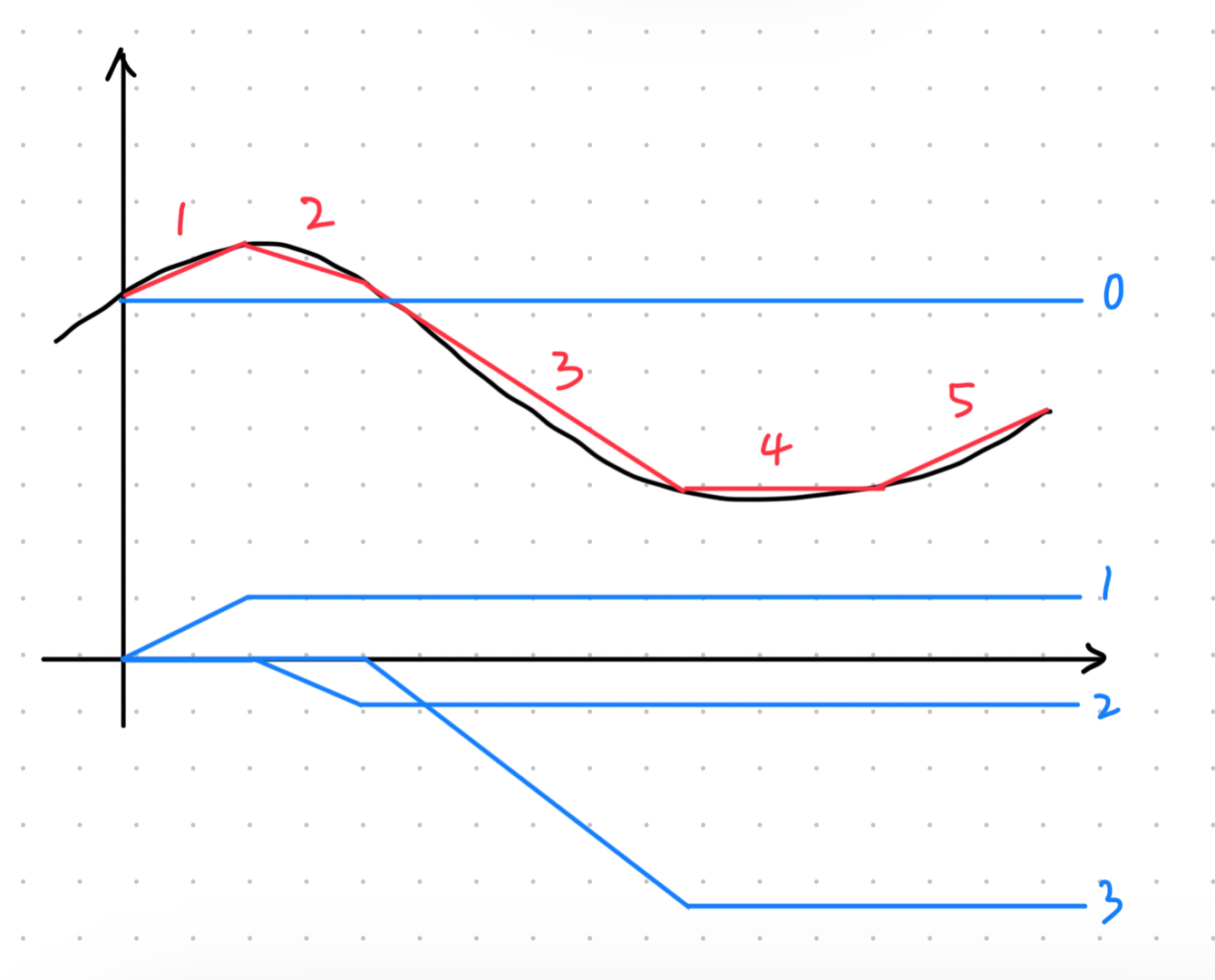
如下圖所示，假設我們想要模擬出黑色曲線，我們可以先用一堆的紅色直線 (下稱紅線) 來逼近它，然後我們可以再用一些形式類似的藍色線來得出紅線。

不難看出，紅線 1 可以由藍線 0 + 1 組成，而紅線 1 + 2 可以由藍線 0 + 1 + 2 組成，以此類推可以將整條紅線用各種藍線組合而成。簡單來說可以寫成這樣: All piecewise linear curves (紅線) = constant (藍線 0 離 x 軸的距離) + sum of a set of sigmoid\text{sigmoid} (藍線)

Sigmoid Function

由於我們很難直接用函數來表達這種藍線(是可以，但不好做)，因此這裡可以用另一種長的很像的函數來逼近，也就是 Sigmoid function，它的數學式長這樣:

y=c⋅11+e−(b+wx1)=c⋅sigmoid(b+wx1)y = c\cdot{1 \over 1 + e^{-(b + wx_1)}} = c\cdot\text{sigmoid}(b + wx_1)

而被 Sigmoid 逼近的藍色直線函數則被稱為 Hard Sigmoid。

最後我們就能將原本的 linear model 進化成紅線的樣子，並得出它的數學式:

y=b+∑ici⋅sigmoid(bi+∑jwijxj)y = b + \sum_i c_i\cdot\text{sigmoid}\left(b_i + \sum_j w_{ij}x_j\right)

用圖來表示的話：

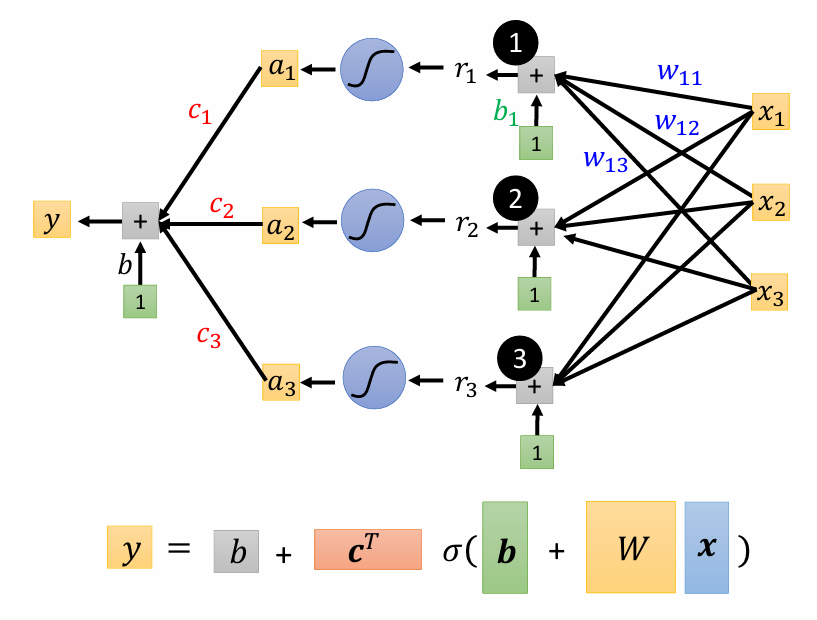source: 李宏毅教授 機器學習 2021 簡報

這裡每一個 xjx_j 都是我們的 feature，而未知參數則有 wij,bi,ci,bw_{ij}, b_{i}, c_{i}, b，我們可以將這些未知參數都統一放到一個矩陣內，稱作 θ\theta。

θ=[w11w12⋮b1⋮]=[θ1θ2θ3⋮]\theta = \begin{bmatrix} w_{11} \\w_{12} \\\vdots \\b_1 \\\vdots \\\end{bmatrix}=\begin{bmatrix}\theta_{1}\\\theta_{2} \\\theta_{3} \\\vdots \\\end{bmatrix}

定義 Loss & Optimization

首先一樣定義出 Loss L(θ)L(\theta)，接著我們要找到有著最小的 Loss 的 θ∗\theta^*。

在 Optimization 的部分，我們之前是由整個訓練資料 NN 得出一個 LL，整個過程都使用該 LL 做計算。不過這次我們會將 NN 隨機分成幾塊大小一樣的 batch BB，然後每次都使用不同的 B 來得出不同的 LL。具體步驟如下：

  1. 隨便取一個初始值 θ0\theta^0
  2. 使用 B1B^1 的資料得出 L1L^1 並計算 gradient:
g=∇L1(θ0)=[dLdθ1∣θ=θ0dLdθ2∣θ=θ0⋮]g = \nabla L^1 (\theta^0) = \begin{bmatrix}{dL \over d\theta_1}|_{\theta = \theta_0} \\{dL \over d\theta_2}|_{\theta = \theta_0} \\\vdots\end{bmatrix}
  1. 更新 θ\theta 的值:
θ1=θ0−η⋅g\theta^1 = \theta^0 - \eta\cdot g
  1. 使用 B2B^2 的資料得出 L2L^2 並計算 gradient:
g=∇L2(θ0)g = \nabla L^2 (\theta^0)
  1. 更新 θ\theta 的值:
θ2=θ1−η⋅g\theta^2 = \theta^1 - \eta\cdot g
  1. 重複計算 gradient 並更新 θ\theta，每次更新稱作一次 update，當每個 batch 都被用過一次後稱作一個 epoch，然後再重新回到 B1B^1

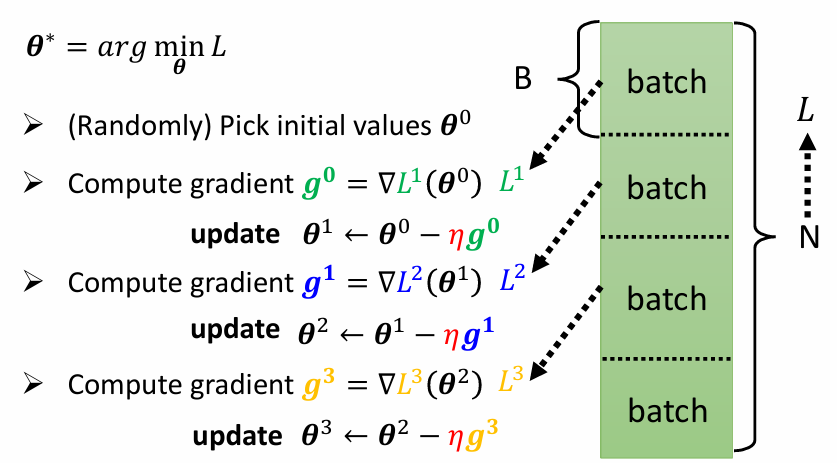source: 李宏毅教授 機器學習 2021 簡報

Activation Function

除了 Sigmoid，我們也可以用其他的函數來逼近藍色線，像是 Rectified Linear Unit (ReLU)，它的數學式如下:

y=c⋅max⁡(0,b+wx1)y = c\cdot \max(0, b + wx_1)

而我們需要兩個 ReLU 才能合成一個 Hard Sigmoid，所以最後的 model 長這樣:

y=b+∑2ici⋅max⁡(0,bi+∑jwijx1)y = b + \sum_{2i} c_i\cdot \max\left(0, b_i + \sum_j w_{ij}x_1\right)

在機器學習裡面，像是 Sigmoid、ReLU 這類在 model 中讀取輸入並換算的函數被稱為 activation function。

深度學習 = 讓機器找 function，但很多層

當然，我們可以把不同的 activation function 組合成一層一層的網路，我們可以先用 Sigmoid 做換算，再用 ReLU 做一次換算，這樣一來就可以獲得更複雜的模型，如下圖所示:

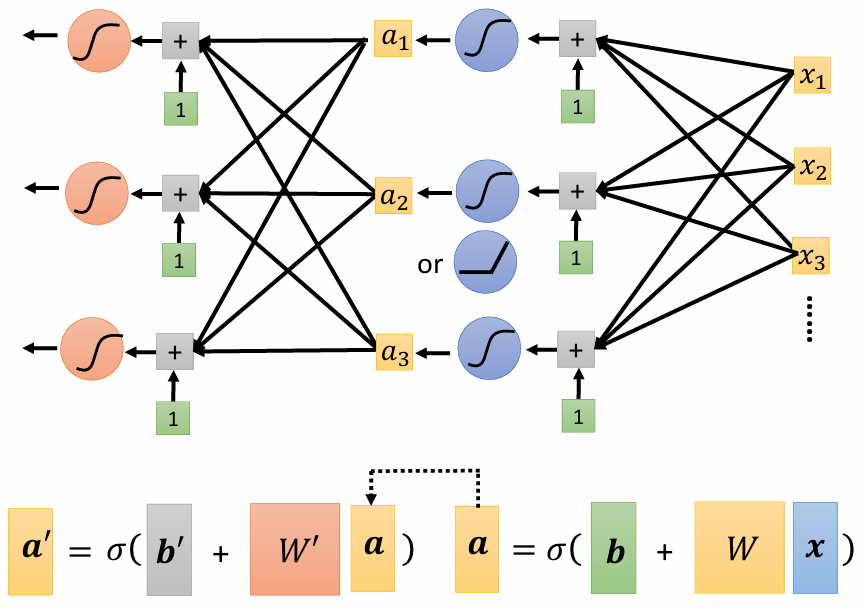source: 李宏毅教授 機器學習 2021 簡報

而這每一層的 activation function 組合起來叫做一個 Neuron，很多的 Neuron 組合起來就是一個 Neural Network。

但是後來這個名字被用得太多，所以後來我們又給了它們新名字，Neuron 改名叫 Hidden Layer，而很多 Layer 就代表這個網路很深，於是這項運用很多層 hidden layer 來進行機器學習的技術就叫 Deep Learning。

但是，實際上即便只有一層，用足夠多的 activation function 也可以很逼近我們想要的 function，那為什麼不做 "Fat Network" 而要做 "Deep Network"？