早上好暑假，現在我有李宏毅教授的【機器學習 2021】系列影片，因為非常好影片，內容非常好。
以下是本篇筆記所參考的影片：
【機器學習2021】機器學習任務攻略 - YouTube

步驟

• Training data (size $N$): $\{(x^1,\hat{y}^1), (x^2,\hat{y}^2), \cdots, (x^N,\hat{y}^N)\}$
• Training:
  1. Function $y = f_{\theta}(x)$ with unknown parameters $\theta$
  2. Define loss from training data $L(\theta)$ → determine the function is good or not
  3. Optimization → find $\theta^* = \arg\min_{\theta}\ L$
• Testing data (size $M$): $\{x^{N+1}, x^{N+2}, \cdots, x^{N+M}\}$
  • Use $y = f_{\theta^*}(x)$ to label the testing data

如果 testing data 的 loss 很小，那就代表這個 model 是不錯的🙂
但如果不是的話，我們就要來修正 model 了🙁

Loss on training data is Large

1. Model bias

模型太簡單，無論怎麼參數怎麼組合都無法描述 $f^*$ (loss 最低的函數) → 讓 model 的彈性更大

1. 增加 features

2. 增加 layers (deep learning)

2. Optimization issue

即便我們的 model 夠複雜，但是我們的 optimization method (i.e. gradient descent) 無法找到 $f^*$ → 更好的 optimization method (待下回分解)

如何判斷是哪一種？

→ 對不同的 model 做比較 從比較容易 optimize 的簡單小 model 出發，像是 linear model 或是低 layer 接著如果較複雜的 model 的 training data loss 沒有比較小，那代表是 optimization issue

Loss on training data is Small, but Loss on testing data is large

1. Overfitting

⚠️ 前提是 training data loss 要夠小

當 model 的彈性大時，在 training data 的資料點上因為有限制所以可以契合的很好，但在 training data 之外的資料點可能會「自由發揮」，導致 loss 變大

解法:

1. more training data (減少可以自由發揮的空間)
   • 直接用現有的資料
   • 根據問題自己生新的 (data augmentation)
2. constrained model (加上限制，減少彈性)
   • Less parameters、sharing parameters
   • Less features
   • Early stopping
   • Regularization
   • Dorpout

如何挑選 model

前面提到我們可以透過加上限制來解決 overfitting，但如果限制太多，又會回到 model bias，這是一個 bias-complexity trade-off

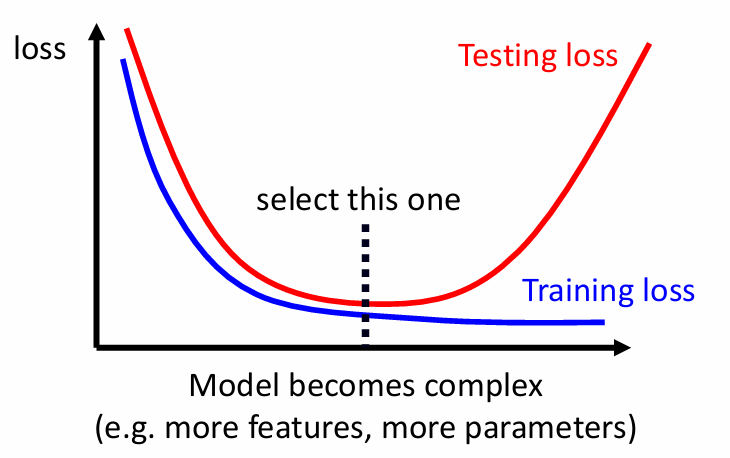source: 李宏毅教授 機器學習 2021 簡報

→ 解法: Cross Validation 將 training data 分成 training set 和 validation set

→ 如何分: N-fold Cross Validation

1. 將 training data 切成三等份，其中一份當 validation set
2. 循環三次，每次都取不同的當 validation set
3. 將三次的分數取平均

2. Mismatch

training data 和 testing data 的分布根本不同，因此無論如何增加 training data 都無濟於事。舉例來說，training data 是彩色圖片但 testing data 是黑白圖片。