blog logo
Blog
李宏毅機器學習筆記 (三) - 如何優化訓練方法

早上好暑假，現在我有李宏毅教授的【機器學習 2021】系列影片，因為非常好影片，內容非常好。
以下是本篇筆記所參考的影片：
【機器學習2021】類神經網路訓練不起來怎麼辦 (一)： 局部最小值 (local minima) 與鞍點 (saddle point) (youtube.com)
【機器學習2021】類神經網路訓練不起來怎麼辦 (二)： 批次 (batch) 與動量 (momentum) (youtube.com)
【機器學習2021】類神經網路訓練不起來怎麼辦 (三)：自動調整學習速率 (Learning Rate) (youtube.com)

以下皆使用 gradient descent 來探討

練到卡住了: Critical Point

當 gradient ≈\approx 0 的時候，無論 update 怎麼提高，training loss 都不太會減少，而 gradient ≈\approx 0 的點稱為 critical point，而 critical point 可能發生在兩種情形:

  • local minima
  • saddle point (有機會從旁邊 escape)

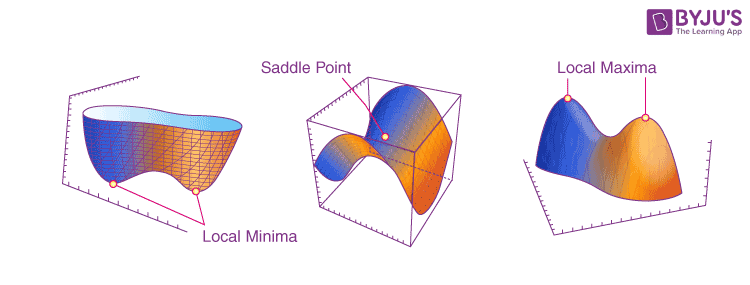|500 source of figure: Saddle Points | Saddle Points in Multivariable Function (byjus.com)

如何判斷是哪一種？

給定某個 θ′\theta' 來估計 L(θ)L(\theta) 在 θ=θ′\theta = \theta' 附近的形狀，使用 Taylor series approximation 如下 (式子一):

L(θ)≈L(θ′)+(θ−θ′)Tg+12(θ−θ′)TH(θ−θ′)L(\theta) \approx L(\theta') + {\color{red}(\theta - \theta')^Tg} + {\color{blue}{1 \over 2}(\theta - \theta')^TH(\theta - \theta')}

其中 Gradient gg 是一個向量，Hessian HH 是一個矩陣:

gi=∂L(θ′)∂θiHij=∂2∂θi∂θjL(θ′)g_i = {\partial L(\theta') \over \partial\theta_i}\quad\quad\quad H_{ij} = {\partial^2 \over \partial\theta_i\partial\theta_j}L(\theta')

因此當 g=0g = 0 的時候，紅色的部分也會是 0，我們就可以透過藍色的部分來判讀附近的地形。

以下先用 vv 來代替 θ−θ′\theta - \theta' 這個向量，如果 vTHv>0v^THv \gt 0 for all vv，也就是說 θ′\theta' 的附近 L(θ)>L(θ′)L(\theta) \gt L(\theta')，所以很明顯是 local minima，但我們很難對所有 vv 作嘗試，因此可以用 eigen value 來判斷:
vTHv>0v^THv \gt 0 for all vv → HH is positive definite → all eigen values are positive

以此類推:

  • All eigen value are positive → local minima
  • All eigen value are negative → local maxima
  • Some positive, some negative → saddle point

如何逃脫 saddle point

繼續用上面的式子，假設 HH 有一個 eigen vector uu，然後對應的 eigen value 是 λ\lambda，則我們可以得出:

uTHu=uT(λu)=λ∥u∥2u^THu = u^T(\lambda u) = \lambda\lVert{u}\rVert^2

假設 θ=θ′+u\theta = \theta' + u，也就是 θ′\theta' 沿著 uu 的方向做更新，則上面的式子一 (g=0g = 0) 就變成:

L(θ)≈L(θ′)+12uTHuL(\theta) \approx L(\theta') + {1 \over 2}u^THu

如果 λ<0\lambda \lt 0 → uTHu<0u^THu \lt 0，則我們就得到更低的 loss:

L(θ)<L(θ′)L(\theta) \lt L(\theta')

結論: 卡在 saddle point 得時候，找出一個負的 eigen value λ\lambda，再找出對應的 eigen vector uu，將新的 θ\theta 更新成 θ′+u\theta' + u，就能獲得更低的 loss。

實務上我們並不會用上述的方法，因為同時對 HH 做二次微分還要找 eigen value 是相當大的運算量，實際上還有更多運算量更低的方法。

local minima 比想像中的少？

當我們將三維的 saddle point 以二維的視角觀看時，它其實會像是一個 local minima (or maxima)，也就是說，維度不同可能也會改變它是不是一個 local minima，當維度越高的時候，原本的 local minima 就越有可能「不是」local minima。

實作上，其實也很難找到真的 local minima (all eigen value are positive)，大多數的時候 eigen value 都是有正有負 (saddle point)。

優化: 挑選 Batch Size

直覺上來看，我們會以為 large batch 是 cd 長的精準攻擊，而 small batch 是 cd 短的亂槍打鳥，然而實際上卻不一樣。

Compute Time

當 batch size 在一定大小內，每次 update 的時間其實差不多 (因為可以做平行運算)，但超過限制後就會變超大；相對的 batch size 越小，每個 epoch 的時間就越長。

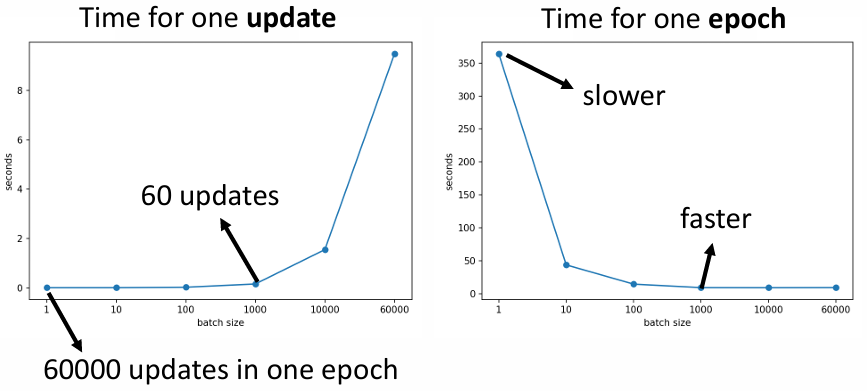|500 source of figure: small-gradient-v7.pdf (ntu.edu.tw)

Accuracy

就結果而言，large batch 的 training accuracy 反而下降。
可能的解釋: large batch 在算到 g=0g = 0 時就會停下；而 small batch 因為每一次都會用不同的 loss 來算 gradient，即便在 L1L_1 上算出了 g=0g = 0，下一步使用 L2L_2 計算時則不一定，因此可以繼續算下去 (得到更好的 loss)。

即便今天把 large batch 的 training accuracy 算到和 small batch 差不多，large batch 的 testing accuracy 也不會太好 (overfitting)。
可能的解釋: 首先，local minima 有分成兩種，sharp minima 比較不好，flat minima 比較好，原因是因為 sharp minima 在 training loss 和 testing loss 之間可能出現較大的差距 (見圖)。

|500

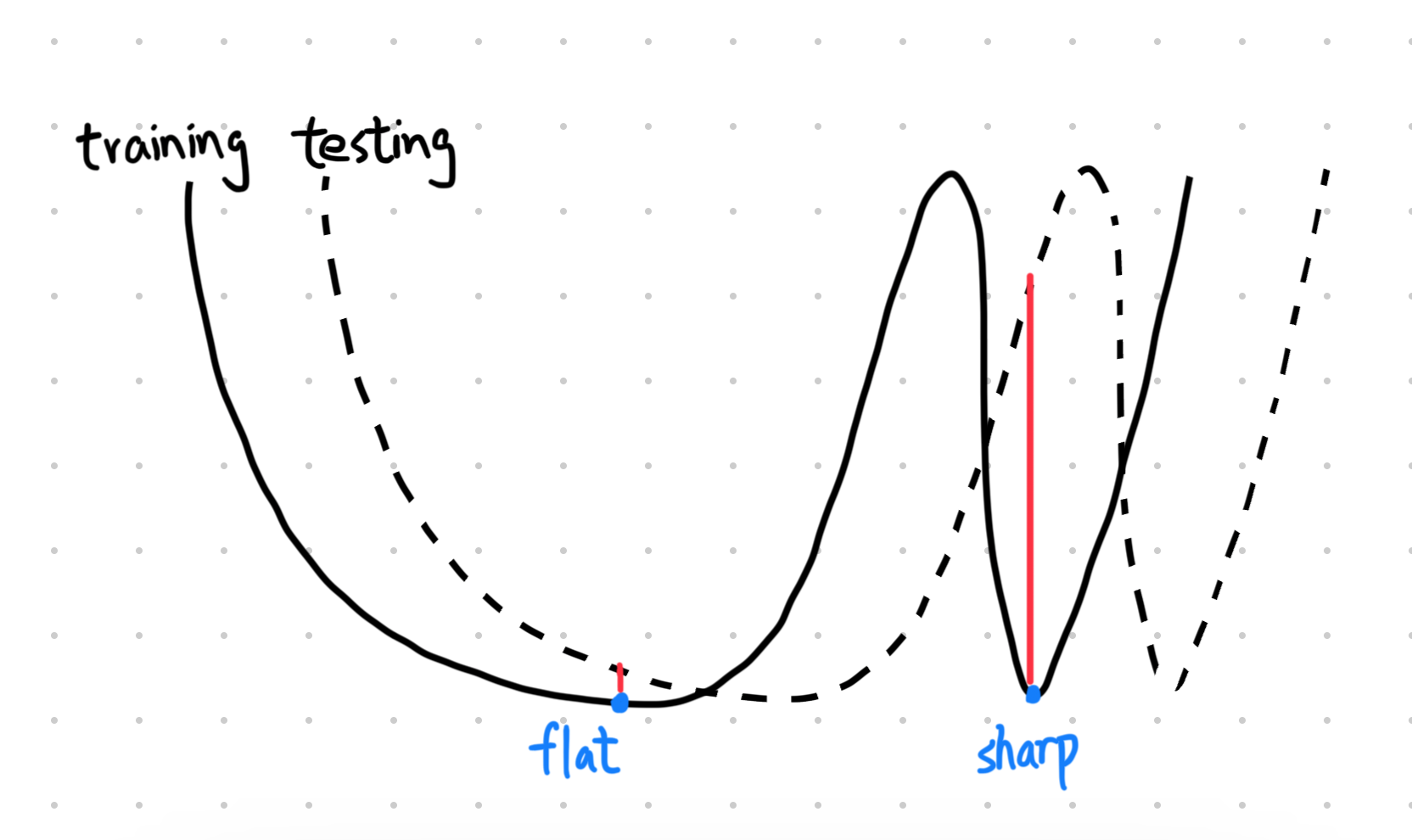
而 small batch 因為每次更新的 gg 比較隨機，因此比較容易逃脫 sharp minima。

Overall Comparison

smalllarge
Speed for one update (with parallel)samesame (沒差多少)
Time for one epochslowerfaster
Gradientnoisystable
Optimizationbetterworse
Generalizationbetterworse

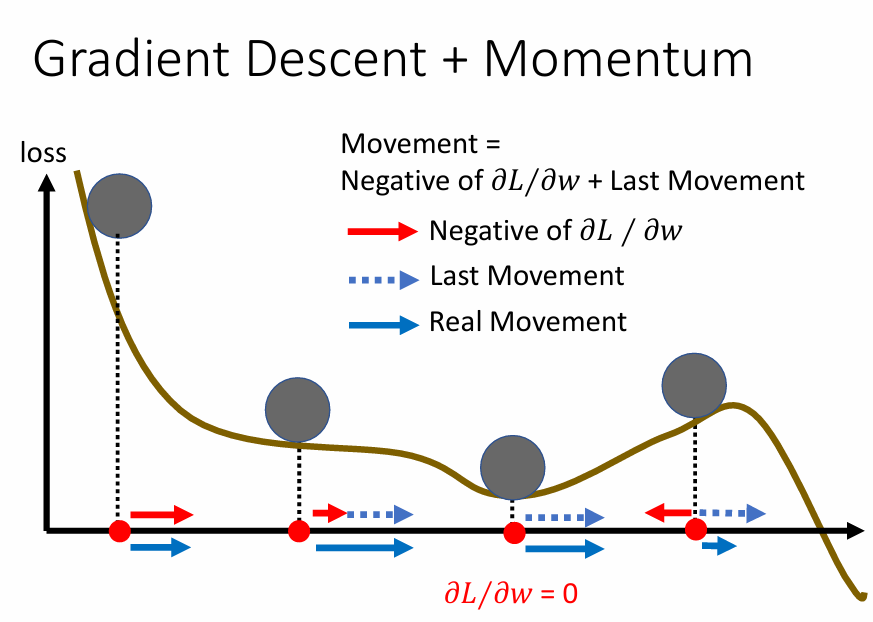
優化: 加上 Momentum

考慮物理上的情況: 將球從高處滾下，因為有 momentum，所以球不一定會被 local minima 給卡住

將這個概念運用到 gradient descent 上:

|500 source of figure: small-gradient-v7.pdf (ntu.edu.tw)

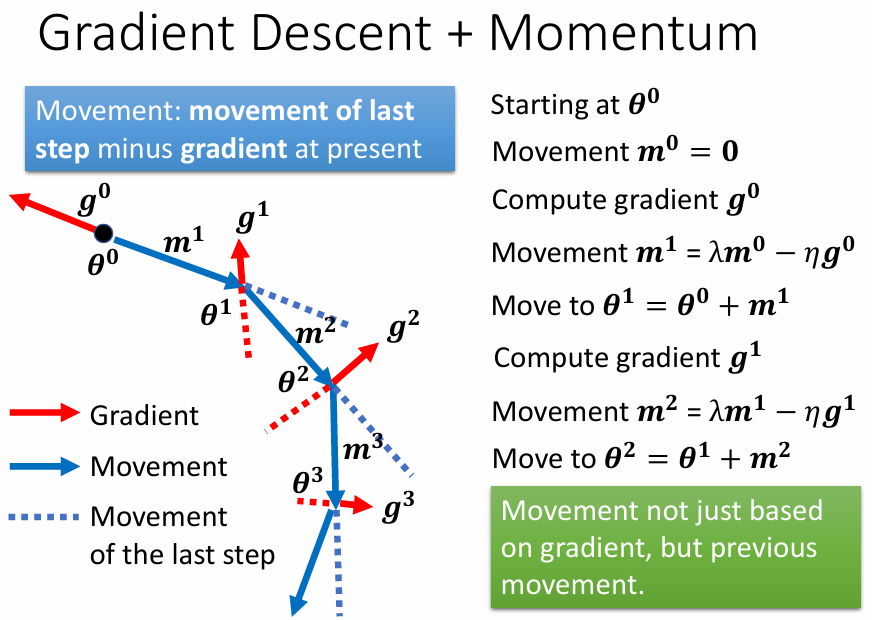|500 source of figure: small-gradient-v7.pdf (ntu.edu.tw)

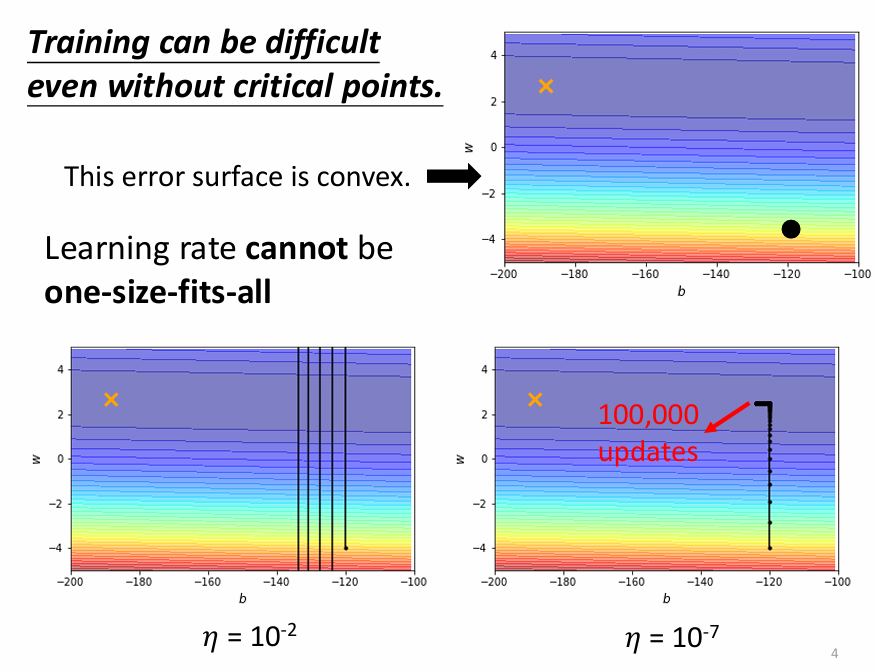
練到卡住不見得是 critical point

事實上，在訓練的過程中卡在 critical point 的情況很少，往往在還沒碰到 critical point 之前就卡住了。以下圖為例，error surface 在沿 y 軸方向的 gradient 變化比較大，但沿 x 軸方向的 gradient 幾乎沒有變化。在 learning rate 大的時候，在 y 軸方向很容易找不到谷底而持續在兩端反彈；而 learning rate 小的時候，雖然能找到谷底，在 x 軸方向卻因為斜率沒有變化而進度緩慢。

|500 source of figure: optimizer_v4.pdf (ntu.edu.tw)

優化: 動態 learning rate

不同參數用不同 learning rate: RMS

對不同的參數 ii，我們要使用不同的 learning rate η\eta，因此原本更新 θ\theta 的方式變成:

θit+1=θit−ησitgit\theta^{t+1}_{i} = \theta^{t}_{i} - {\eta\over\sigma^{t}_{i}}g^{t}_{i}

其中 σ\sigma 是用來調整 learning rate 的參數，要怎麼計算 σ\sigma 則由我們自己決定，常用的方法有計算 gradient 的 RMS(root mean square)，如下:

σit=1t+1∑i=0t(git)2\sigma^t_i = \sqrt{{1\over t+1}\sum^t_{i=0}{(g^t_i)}^2}

這樣一來，我們就可以在 gradient 小的時候調大 learning rate，vice versa。

同一個參數也可以用不同 learning rate: RMSProp

然而，即便是同一個參數在同個方向的 gradient 也可能不同，因此有了更進階的版本:

σit=α(σit−1)2+(1−α)(git)2\sigma^t_i = \sqrt{\alpha{(\sigma^{t-1}_i)}^2 + (1-\alpha){(g^t_i)}^2}

其中 α\alpha 是一個 hyperparameter，用來決定當下的 gig_i 以及之前的 g1g_1 ~ gi−1g_{i-1} 分別對目前 σit\sigma^t_i 的影響力。舉例來說，常用的 optimizer 像是 Adam 就使用了 RMSProp 和 Momemtum 來做優化。

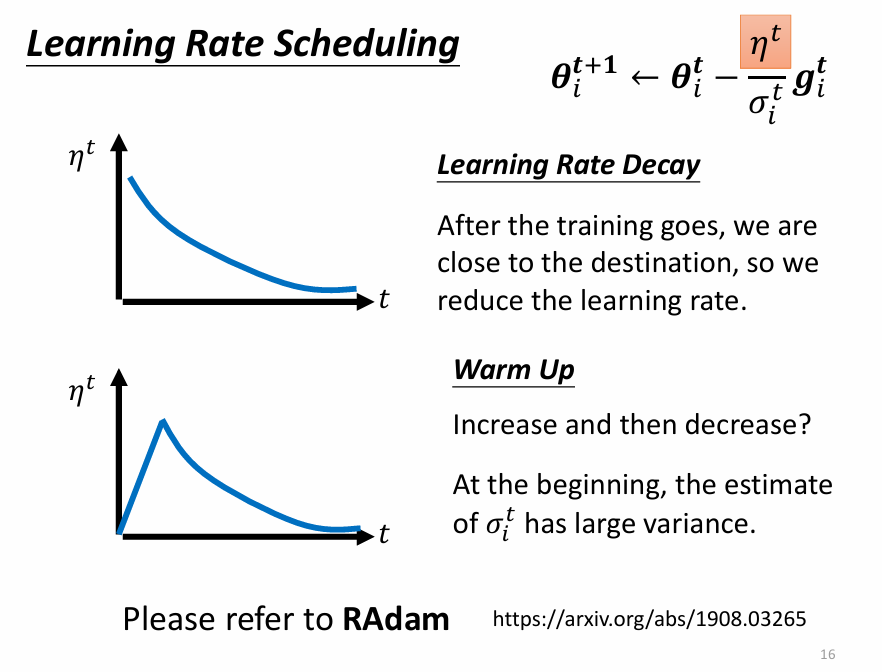
隨時間調整 learning rate: Learning Rate Scheduling

source of figure: optimizer_v4.pdf (ntu.edu.tw)

優化方法總結

source of figure: optimizer_v4.pdf (ntu.edu.tw)