早上好暑假，現在我有李宏毅教授的【機器學習 2021】系列影片，因為非常好影片，內容非常好。
以下是本篇筆記所參考的影片：
【機器學習2021】類神經網路訓練不起來怎麼辦 (四)：損失函數 (Loss) 也可能有影響 (youtube.com)
【機器學習2021】類神經網路訓練不起來怎麼辦 (五)：批次標準化 (Batch Normalization) 簡介 - YouTube

做 Classification 時的優化

Classification as Regression

假設我們想預測身高和年級的關係，每個年級都是一個 class，那這時候或許可以將 classification 使用 regression 的方式來處理，只要將輸出的每個 scalar $y$ 都對應到一個 class $y$ 就行。我們的終極目標是讓輸出的 $y$ 離正確答案 $\hat{y}$ 越接近越好，由於 class 之間在我們想預測的變量(身高)上是有關係的，一年級和二年級的身高會比一年級和三年級接近，所以我們可以判斷 class 之間的「差距」。

但假如 class 之間沒有這類關係的話，例如我們想判斷一張圖片是哪種水果，此時很難判斷 $y$ 和 $\hat{y}$ 之間的「差距」，因為我們不能說蘋果和橘子之間的差距大於蘋果和香蕉之間的差距。

Class as one-hot vector

比較常見的做法使用 one-hot vector 來表示不同 class:

\hat{y} = \begin{bmatrix}1\\0\\0\end{bmatrix}\text{(class 1)}\ \text{or}\ \begin{bmatrix}0\\1\\0\end{bmatrix}\text{(class 2)}\ \text{or}\ \begin{bmatrix}0\\0\\1\end{bmatrix}\text{(class 3)}

這樣一來每個 class 之間的距離都是一樣的，因此 classification 的 network 會長得像這樣:

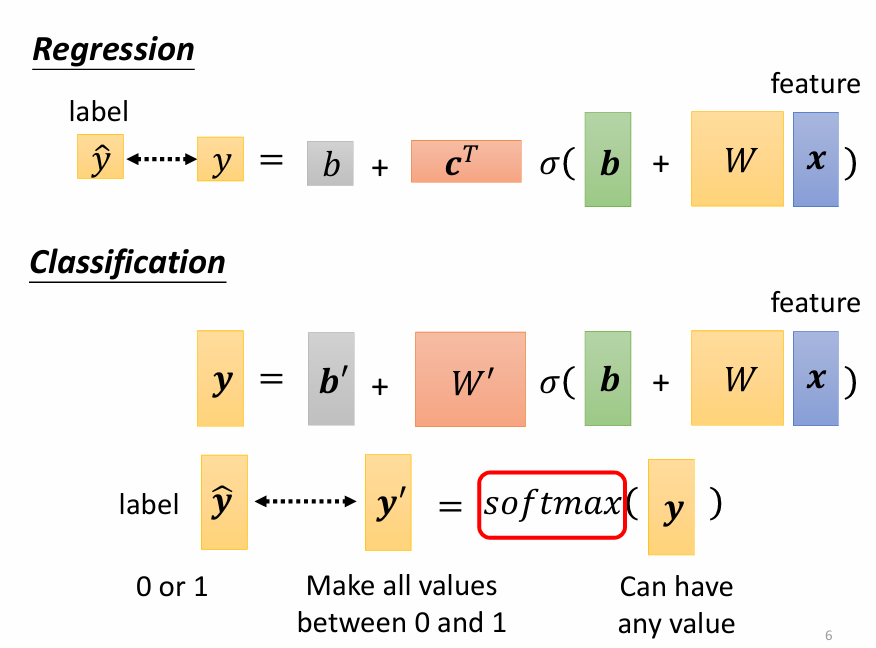|500 source of image: classification_v2.pdf (ntu.edu.tw)

此時 $y$ 是一個向量，而由於 $\hat{y}$ 都介於 0 和 1 之間，因此我們要透過 softmax 這個函數來將 $y$ 轉換成 0 和 1 之間的數值 $y'$ 。而 softmax 的運作方式如下:

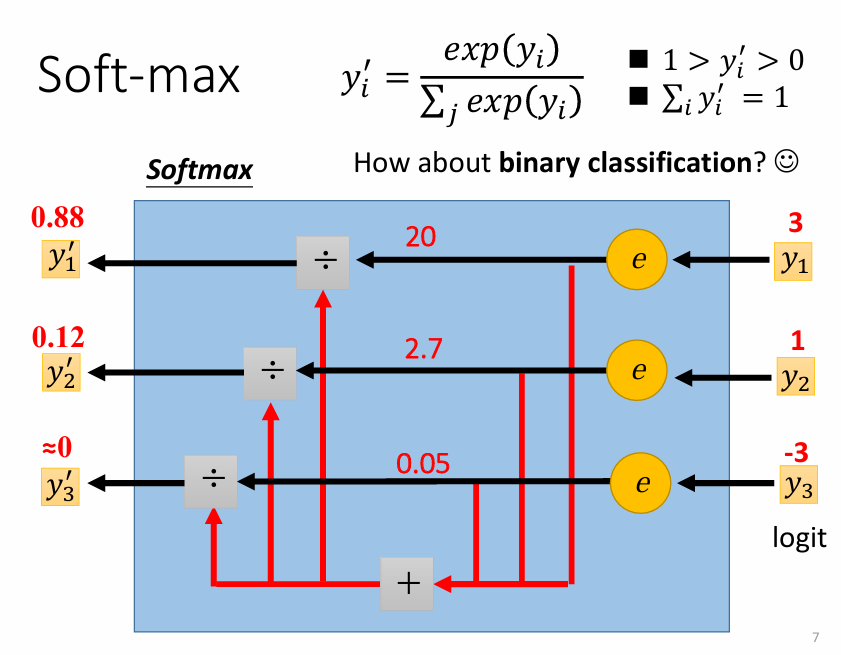|500 source of image: classification_v2.pdf (ntu.edu.tw)

上面是考慮三個 class 的情況，但在兩個 class 的情況下，直接取 sigmoid 和做 softmax 是一樣的事情。(我不會證)

Loss of Classification

在做 classification 的時候，比較常使用 cross-entropy 來計算 loss ( $y'$ 和 $\hat{y}$ 的差距)，數學式如下:

e = - \sum_i{\hat{y}_i\ln{y'_i}}

Minimizing cross-entropy is equivalent to maximizing likelihood

Batch Normalization

不好的 error surface

如果今天 feature 內不同 dimension 的數值分布差異很大，就會導致它們對 loss 的影響程度不同，也就會產生不同方向上斜率差異很大的 error surface (如下圖的藍色曲線)。

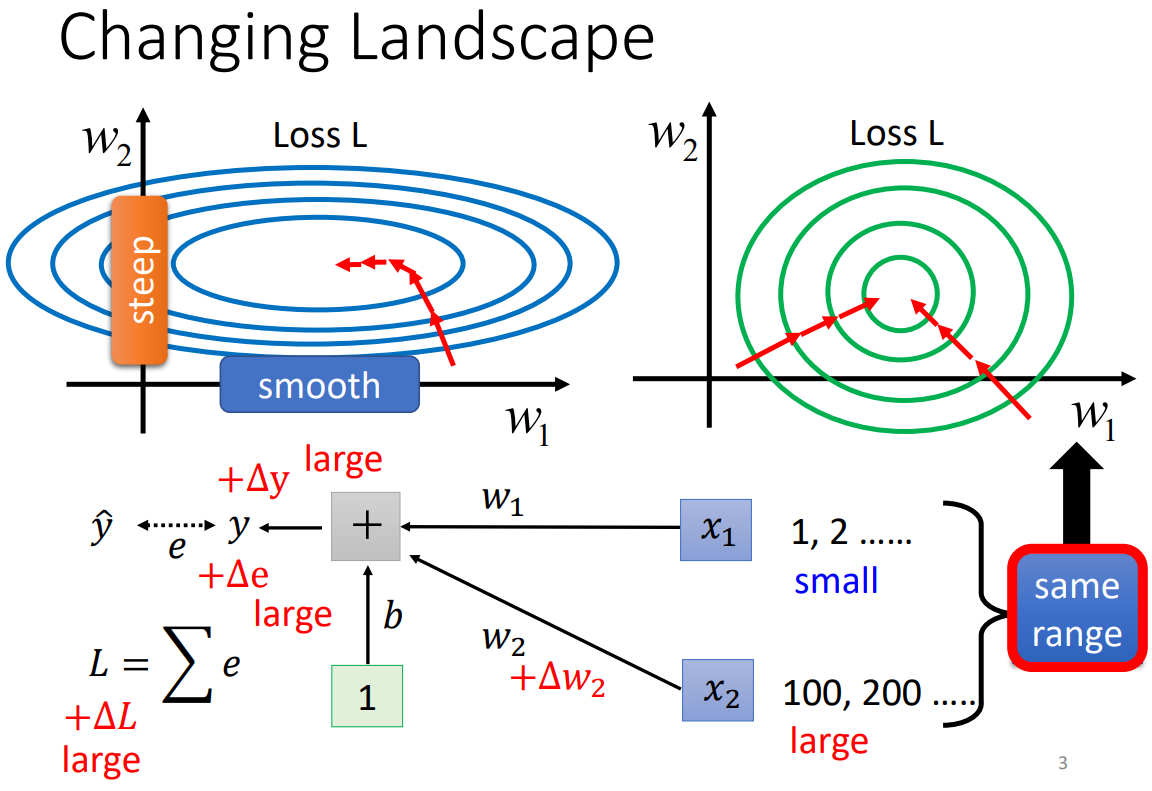|500 source of image: Batch Normalization (ntu.edu.tw)

Feature Normalization

要解決這個問題，我們可以透過 Feature Normalization 這類方法來讓不同 dimension 有相近的數值分布，以下只講述其中一種方法: Standardization，就是將每個 dimension 的平均 ( $\mu$ ) 都變成 0、標準差 ( $\sigma$ ) 變成 1。Normalization (standardization) 後的值為:

\tilde{x}_i^r = {x_i^r-\mu_i \over \sigma_i}

其中 $i$ 是 dimension、 $r$ 代表不同的 example、 $\tilde{x}$ 表示被 normalization 後的值。

註：以下的 normalization = standardization

而 feature $\tilde{x}$ 在經過 weight 計算後得出的 $z$ 其實也需要做 normalization，方法跟之前很像。(下圖的 $z, \mu, \sigma$ 都是向量)

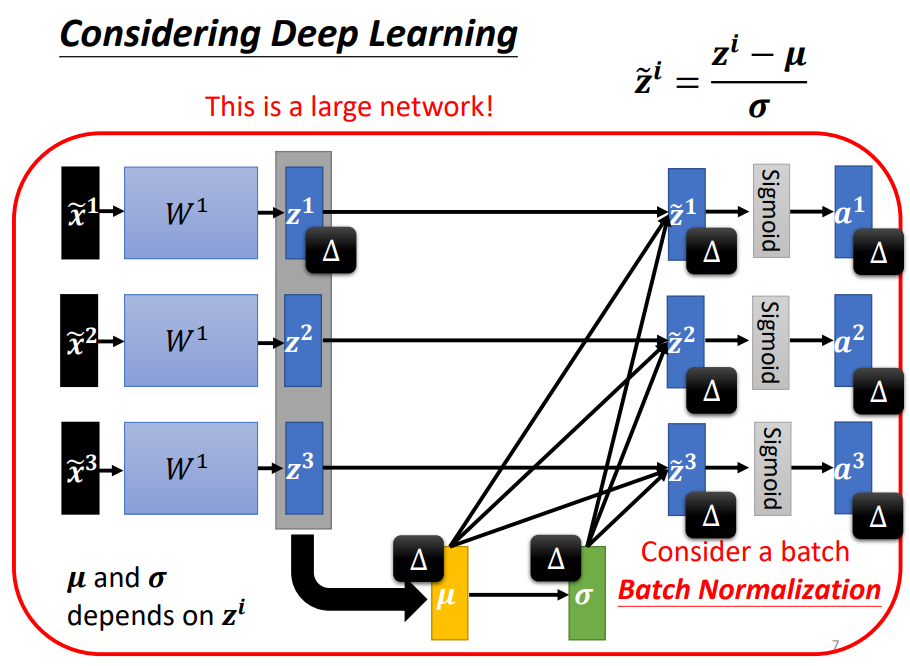|500 source of image: Batch Normalization (ntu.edu.tw)

對 $z$ 做了 feature normalization 後，原本不會互相影響的 $z$ 變成會互相影響了，也就是說一旦 $z^1$ 有了變化，算出來的 $\tilde{z}^2, \tilde{z}^3$ 也會改變，因此我們需要將整個過程視為一個大 network。

既然它是一個 network，我們處理每一筆 example 都必須一次輸入全部的 $\tilde{x}^i$ (因為會互相影響)，但現在一個 data 動輒上百萬筆資料，我們沒辦法一次 load 這麼多的資料，因此我們一次只對一個 batch 內的資料做 normalization。

Batch Normalization

對 batch 做 normalization 時，為了可以調整輸出的分布，通常還會多加一個步驟:

\hat{z}^i = \gamma\odot\tilde{z}^i + \beta

最一開始的時候，為了讓每個 dimension 維持相近的分布，會先把 $\gamma$ 設為一向量、 $\beta$ 設為零向量，後續再慢慢調整。

Testing (Inference)

在實際上 testing 的時候，我們很難對輸入做 batch normalization，不可能等到累積到一個 batch 的資料後才開始做運算，那如果沒有 batch 要怎麼算 $\mu, \sigma$ 呢？

因此在 training 的時候，我們會使用每一個 batch 算出來的 $\mu^i$ 來更新 moving average $\bar{\mu}$ 的值:

\bar{\mu} = p\bar{\mu} + (1-p)\mu^i

最後 testing 的時候就會直接使用最後算出來的 $\bar{\mu}$ 。

實際上 batch normalization 為什麼會有用，仍沒有一個定論，而除了 batch normalization 之外其實還有更多的 normalization 方法。