注意！此筆記的作者沒有經過任何專業的統計學教育，所有知識皆由網路自學，因此內容可能有些錯誤，請小心閱讀。

一些基本名詞

Population (母數、母體): 所有你有興趣的對象群體，假設你想要研究大學生對統計學的喜好度，那這個研究的 population 就會是全部的大學生。通常 population 會很大，所以我們不會直接對 population 做研究。

Parameter (參數): 用來形容 population 的數值，像是 mean, median, standard deviation 等

Sample (樣本): 透過 CLT，我們可以從 population 中取出一些 samples 來代表整個 population。基本上 samples 就是 population 的 subset，通常都是針對 sample 做研究。

Central Limit Theorem (CLT) 對於任何 population 取出 n 個 samples 時，當 n 夠大時 (通常是 n > 30)，這些 samples 的平均數的 distribution 會趨近於 normal distribution；也就是說，這些 samples 的平均數會相當於 population 的平均數。

Statistic (統計量): statistic 之於 sample 相當於 parameter 之於 population。

Distribution (分布): 一個函數，會把變數 $a$ 的所有可能值 $F_X(a)$ 對應到這個值發生的機率 $P(X \le a)$ 。Distribution 的種類很多，還有分 discrete 和 continuous，但這偏機率了，以後有機會整理機率筆記再說。

註: 這裡的 $X$ 是 random variable，這是一個把實驗的所有結果對應到任意實數的函數。舉例來說， $X(\text{沒抽到鬼牌}) = 0$ 、 $X(\text{抽到鬼牌}) = 1$ 。

68-95-99.7 Rule: 如其名，在 normal distribution 中:

離平均值一個標準差內的數據佔整體的 68.27%
離平均值兩個標準差內的數據佔整體的 95.45%
離平均值三個標準差內的數據佔整體的 99.73%

這也延伸出了 Three-Sigma Rule: 幾乎所有的實驗結果(值)都會落在三個標準差 ( $\sigma$ ) 之內，因此大部分的研究都將 99.7% 以上的機率視為「一定」。

假說檢定

背景

註: 對於不同研究，假說的建立、顯著水準的設定、假說檢定的方式都會有差異，這裡只舉了其中一種例子

假設我們現在想要研究: 站著使用 VR 時的舒適度是否低於躺著使用 VR 時的舒適度 為了方便，以下用 A = 站著使用 VR 的情境，B = 躺著使用 VR 的情境

假設我們針對 N=3 名受試者做了研究，結果顯示: A 的舒適度分數為 4, 5, 8；而 B 的舒適度分數為 7, 8 ,10 這樣是否可以說明對於整個 population 而言，A 比 B 不舒服呢？

有沒有可能，有其中一個受試者站著會腰痛，所以才覺得躺著比較舒服？因為無法對整個 population 做實驗，就可能會產生抽樣誤差(剛好找到腰痛的受試者)，那我們要如何說服自己 A 和 B 的差異是來自於 AB 本身而不是來自於抽樣的誤差？

因此這裡就有了Hypothesis testing (假說檢定)。

What is 假說檢定

首先，我們會建立一個針對 population 的 Alternative Hypothesis $H_1$ (對立假說)，通常也就是我們想要證明的結果，在這裡是 A 和 B 的舒適度有顯著差異

但我們不會直接去證明這個 $H_1$ 是正確的，而是透過建立另一個與其相對的 Null Hypothesis $H_0$ (虛無假說)，也就是我們想要的效應不存在，在這個例子中就是 A 和 B 的舒適度沒有顯著差異

然後我們會透過一些統計騷操作 (e.g. t-test, ANOVA)，來看看其結果是否能夠:

說服我們拒絕這個 $H_0$ ，也就是說明 A 和 B 的舒適度實際上是有差異的
結果不足以拒絕 $H_0$ ，而實驗結果的差異只是因為採樣造成的誤差而已。(這裡只能說證據不足以拒絕，不代表 $H_0$ 是正確的)

單尾、雙尾檢定

這裡有個小問題，我們的研究應該是要說明 A 的舒適度顯著低於 B 的舒適度，為什麼 $H_1$ 卻是 A 和 B 的舒適度有顯著差異呢？

如果我們將假說改成這樣 $H_1$ : A 的舒適度顯著低於 B 的舒適度 $H_0$ : A 的舒適度顯著高於或等於 B 的舒適度

那這樣子我們所做的便是 One-Tailed Test (單尾檢定)，這類檢定通常會在研究者很確定(相信)實驗結果的方向性時，也就是我們相信 A 的舒適度一定低於 B 舒適度，而不可能會相反。

然而，One-Tailed Test 就會完全忽略另一個方向的顯著性，如果實際上 A 的舒適度顯著高於 B，那我們獲得的結果。

因此，當我們不確定實驗結果的方向性時，也就是我們相信 A 和 B 會有差異，但不確定是 A 高於 B 還是 A 低於 B，我們就會採用 Two-Tailed Test (雙尾檢定)。這時的假說就會是 $H_1$ : A 的舒適度和 B 的舒適度有顯著差異 (A 的舒適度可能高於或低於 B 的舒適度) $H_0$ : A 的舒適度和 B 的舒適度沒有顯著差異

知道 A 和 B 有差異後，我們再用其他分析去看它的方向性，是 A 低於 B 還是 A 高於 B。

P value 和顯著水準

好，現在我們知道假說檢定的終極目標是要拒絕 $H_0$ ，那我們要怎樣拒絕 $H_0$ 呢？

首先，我們決定要用什麼樣 statistic 來做檢定，這個 statistic 就被稱為我們的 test statistic $T$ (檢定統計量)。接著我們可以透過一些計算，找到「如果 $H_0$ 是正確的， $T$ 的 distribution 會長怎樣」，假設這個 distribution 是 $D_0$ 。

然後我們針對實驗結果也會得到一個 test statistic $t$ ，如果我們可以說明從 $D_0$ 內獲得與 $t$ 相當或是比 $t$ 更極端的數值的可能性非常小，那我們就可以說 $T$ 的分布不太可能是 $D_0$ ，從而拒絕 $H_0$ 。

註：這裡的 $t$ 跟 t value 沒有任何關係，只是剛好我名稱取的很像

注意，上面的「從 $D_0$ 內獲得與 $t$ 相當或是比 $t$ 更極端的數值的可能性」其實就是 $p$ value 的定義:

在 $H_0$ 是正確的前提下，實驗結果等於或比觀察結果( $t$ )更極端的機率

總結來說，我們會用一個 significance level $\alpha$ (顯著水準) 來做為門檻，如果上述情況的可能性小於這個門檻，也就是 $p \le \alpha$ ，我們就可以拒絕 $H_0$ 。通常我們會將 $\alpha$ 定為 0.05 = 5%。

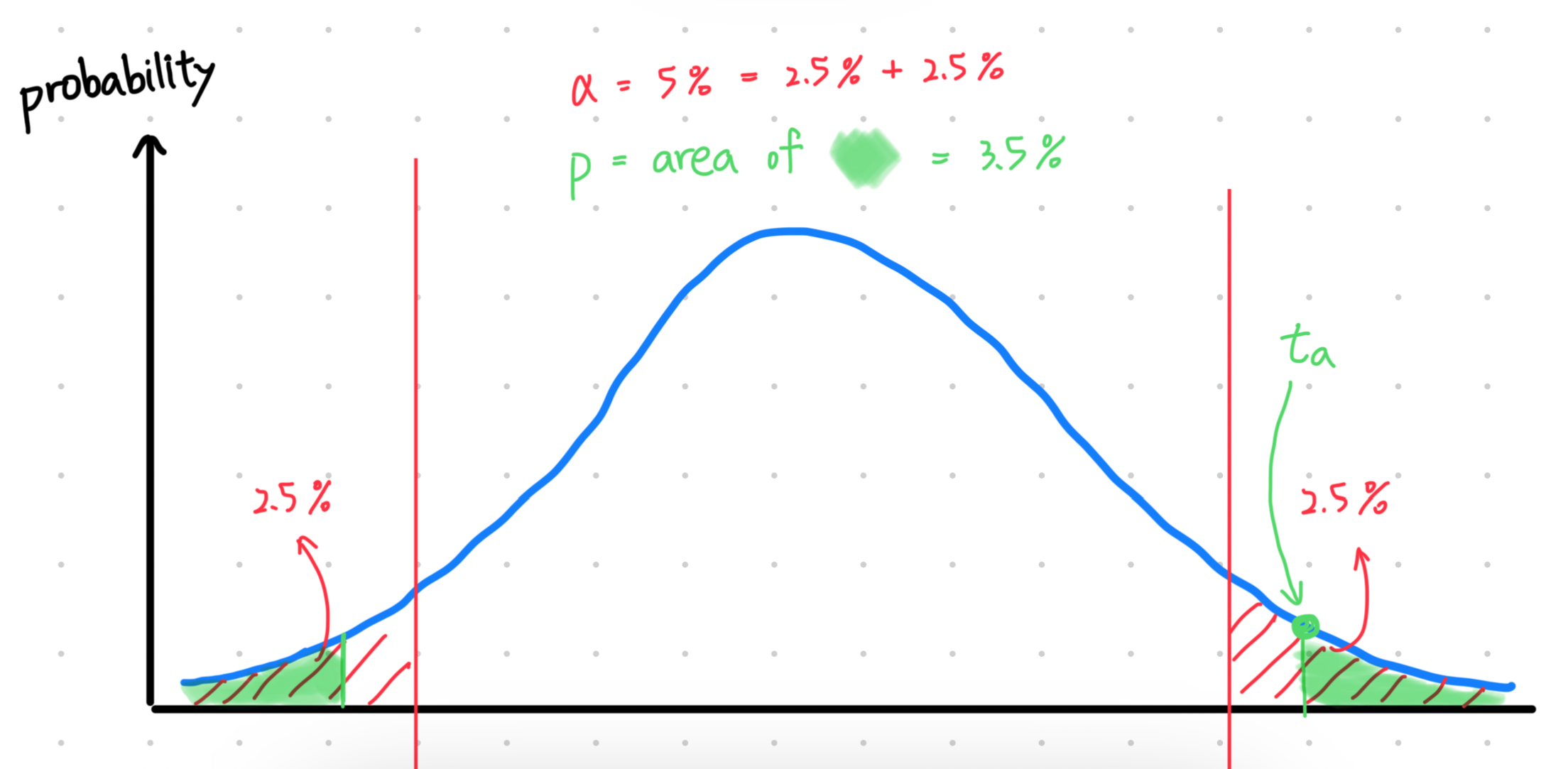圖一：藍色分布是 $D_0$ ，以雙尾檢定為例

同時，顯著水準 $\alpha$ 也代表著 Type I Error (型一錯誤) 發生的機率，為什麼？

首先想想怎樣會發生型一錯誤： $H_0$ 為真的情況下，我們卻拒絕了 $H_0$ ，也就是說，我們的 $t$ 確實是從 $D_0$ 取出來的，而從 $D_0$ 內獲得與 $t$ 相當或是比 $t$ 更極端的數值的可能性 ( $p$ value) 小於 $\alpha$ 。

然後，符合該條件的 $t$ 會落在圖一中的紅色區域，因此從 $D_0$ 內取得這種 $t$ 的機率就是紅色區域的面積 = $\alpha$ 。

這裡多補充一下：

	$H_0$ 為真	$H_1$ 為真 ( $H_0$ 為假)
拒絕 $H_0$	Type I Error (發生機率 $\alpha$ = 顯著水準)	正確判斷 (發生機率 $1-\beta$ = 檢定力)
不拒絕 $H_0$	正確判斷	Type II Error 發生機率 $\beta$

有母數檢定 and 無母數檢定

假說檢定大致上可以分成 Parametric 和 Non-Parametric 兩種。

Parametric tests (有母數檢定) 需要以「母數」為基底去做分析，因此我們需要對這個母數有一定的了解，通常這代表你能夠對母數的分布做出假設。

註：有些文章會說有母數檢定需要假設母數為 normal distribution，但這並不完全正確，實際上你也可以假設母數為其他分布，像是 binomial。不過實際上大多數的有母數檢定方法都是基於母數為 normal distribution 的假設，所以一般上還是會維持這個定義。

為了正確的假設母數的分布，你的樣本數也需要有一定的數量 (通常是 n > 30)。

另一方面，前面有提到大多數的有母數檢定方法都是基於母數為 normal distribution 的假設，而 normal distribution 是一種 continuous distribution，所以大多數的有母數檢定方法也都要求數據是 continuous 的。

由於有母數檢定的要求很多，所以它的結果也會比較有力，然而有些時候，應該說大多數時候，都很難達到這些要求，所以就有了它的低配版: Non-Parametric Tests (無母數檢定)。

註：這裡的有力可以解釋成檢定力較高。

無母數檢定不需要以上的假設，~~講求的就是一個什麼都不需要的精神~~，可以用來分析任何 continuous data 或是 discrete data (會轉換成 rank)，不過它的結果在大多數時候沒有有母數檢定來的有力。

更詳細關於無母數檢定的特色可以看這個網站: 醫學教育基礎統計名詞介紹 (ntu.edu.tw)

挑選檢定方法

注意！以下只是單純提供一種快速的挑選方法，減少我們迷失在大量統計方法的時間，具體能否使用還是需要根據該檢定方法的要求喔。

比較單一樣本與某個值

舉例來說，某台大宣稱其學生 (母體) 平均智商為 180 (某個值)，剛好我們手上有一組某台大學生的智商數據 (樣本)，那我們便可以用這組樣本來驗證母體的平均是否真的為 180。

註：t-Test 就是指 Student's t-Test (司徒頓 t 檢定)

如果我們假設數據是常態分佈，我們可以比較樣本的 mean 和某個值 → One-sample t-Test

🤓: 不過，如果樣本大小 $n \ge 30$ ，或是我們知道母體的標準差 → One-sample Z-Test
如果我們的數據不是常態分佈，我們可以比較樣本的 median 和某個值 → Wilcoxon Signed-Rank Test

比較兩組獨立樣本之間有無顯著差異

舉例來說，我們想要知道男生的身高和女生之間有無顯著差異。

如果我們假設數據是常態分佈，我們可以檢定兩組樣本的 mean 有無顯著差異 → Two-sample t-Test

🤓: 不過，如果樣本大小 $n \ge 30$ ，或是我們知道母體的標準差 → Two-sample Z-Test
如果我們的數據不是常態分佈，我們可以檢定兩組樣本的 median 有無顯著差異 → Mann-Whitney U-Test

比較多組獨立樣本之間有無顯著差異

如果你的獨立樣本有三組以上，像是我們想要知道男生的身高、女生的身高、秀吉 (第三種性別) 的身高之間有無差異。

如果我們假設數據是常態分佈，我們可以檢定多組樣本的 mean 有無顯著差異 → One-way ANOVA

註：ANOVA 聽起來很酷，但其實就只是 Analysis of variance (變異數分析) 的簡稱
如果我們的數據不是常態分佈，我們可以檢定多組樣本的 median 有無顯著差異 → Kruskal-Wallis Test

如果樣本之間不獨立呢？

如果現在有兩組以上的樣本，而(我們認為)在些樣本之間會互相影響，也就是非獨立，那我們就說它們是 Paired Sample (成對樣本)。

這些相關性可以是時間上的，舉例來說，同一組患者在治療前、治療一個月後、治療三個月後的體重，這種同一組樣本在不同時間點的數據又被稱為縱向數據、重複測量數據。

而這些相關性也可以是空間上的，舉例來說，同一組跑者在穿戴 A 跑鞋和 B 跑鞋的速度。

比較成對兩組樣本之間有無顯著差異

舉例來說，我們想要知道同一組足球員在看閃電十一人前後的射門命中率有無變化。

如果我們假設數據是常態分佈，我們可以檢定成對兩組樣本的 mean 有無顯著差異 → Paired-sample t-Test

🤓: 欸，這裡沒有我出場的機會喔
如果我們的數據不是常態分佈，我們可以檢定成對兩組樣本的 median 有無顯著差異 → Wilcoxon Signed-Rank Test

檢測成對樣本之間的相關性

通常在成對樣本之間，我們還會想要知道他們的相關性，舉例來說，我們想要知道同一組人左手肌力和右手肌力的相關性。

如果我們假設數據是常態分佈 → Pearson's Correlation
如果我們的數據不是常態分佈 → Spearman's Rank Correlation

註：一般而言，相關性的研究都是在兩組樣本之間做，如果有三組樣本，我們也會將其拆成 pairwise 的方式，因此以上的方式都是以兩組樣本為基準。

檢測相關係數之間有無顯著差異

有時候，我們可能想要知道兩個相關係數之間有沒有差異，(因為有些相關可能會被忽略，像是 Pearson 就檢測不到非線性的相關)，這時候可以用 Fisher’s Z Test 來看兩個 Pearson 相關係數或兩個 Spearman 相關係數之間的差異。

註：雖然 Fisher's Z transformation 是用來對 Pearson 做轉換的，不過也有文獻將其用在 Spearman 上面。 Spearman Correlation Coefficients, Differences between

結語

暑假時為了要幫實驗數據挑選分析的方法，我才第一次接觸統計學的世界，找了各式各樣的檢定方法覺得腦袋很亂，所以才整理了這篇筆記，希望以後做實驗的時候不會再花太多時間找分析方法。不過這篇筆記也只是一個很簡單的入門整理，其實還有超多檢定方法我沒有去學，之後大三如果有修統計，可能會再整理上來吧。